The points of intersection of the line r = 2a + t (b - c) with the plane r = a + p (b + c) + q (a + 2b - c) is
4a + 3b - 3c
4a - 3b + 3c
The correct Answer is:D
Topper's Solved these Questions
- ADDITION OF VECTORS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - ADDITION OF VECTORS EXERCISE - EXERCISE 1
135 Videos
- ADDITION OF VECTORS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - ADDITION OF VECTORS EXERCISE - EXERCISE 2 SET - 1
10 Videos
- APPLICATIONS OF DIFFERENTIATIONBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - APPLICATIONS OF DIFFERENTIATIONEXERCISE - EXERCISE 2 SET-4 (SPECIAL TYPE QUESTIONS)
15 Videos
Similar Questions
ABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD;BC and AD. Show that →PA+→PB+→PC+→PD=4→PQ, where P is any point.
View SolutionABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD;BC and AD. Show that →PA+→PB+→PC+→PD=4→PQ, where P is any point.
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
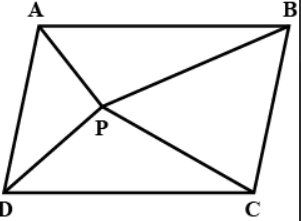
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf p+q+r=0=a+b+c, then the value of the determnalnt |paqbrcqcrapbrbpcqa|is 0 b. pa+qb+rc c. 1 d. none of these
View SolutionIf p+q+r=0=a+b+c, then the value of the determinant ∣∣ ∣ ∣∣paqbrcqcrapbrbpcqa∣∣ ∣ ∣∣is (a)0 (b) pa+qb+rc (c) 1 (d) none of these
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
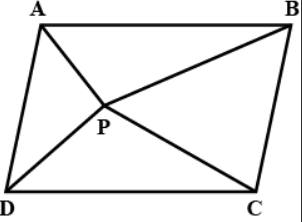
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View Solution
