The work done by force F = ai + j + k in moving a particle from (1,1,1) to (2,2,2) along a straight line is 5 unit. Then a = Solution in Telugu
1
2
3
4
The correct Answer is:C
Step by step video, text & image solution for The work done by force F = ai + j + k in moving a particle from (1,1,1) to (2,2,2) along a straight line is 5 unit. Then a = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PRODUCTS OF VECTORSEXERCISE - Exercise 1B Cross Product of Vectors73videos
PRODUCTS OF VECTORS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PRODUCTS OF VECTORSEXERCISE - Exercise 1C (Triple product of Vectors112videos
PRODUCTS OF VECTORS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PRODUCTS OF VECTORSEXERCISE - Exercise 2 (Special Type Questions) SET -D14videos
PRODUCTS OF VECTORS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PROBABILITYEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-45videos
PROBABILITY
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PROPERTIES OF TRIANGLES EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) Set-410videos
PROPERTIES OF TRIANGLES
Similar Questions
If a = I + j + k, b = 2i - 3j + k then a×b is
05:59View Solution[I - j j - k k - i] =
01:35View SolutionA : Angle between the vectors I - 2j + k, 2i - j - k is π3.
R : If θ is the angle between a,b then cos θ=a.b|a||b|02:05View SolutionA: There are 4 letters and 4 addressed envelopes. If the letters are put in the random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is 3/8.
R: If n letters are put at random in the n addressed envelopes , the probability that all the letters may be in wrong envelopes = 1-11!+12!−13!+.....+(−1)nn!02:05View SolutionA: In a ΔABC, if the sides a,b,c are in A.P. then acos2C2+ccos2A2=3b
R: In a ΔABC, if A,B,C are in A.P. then B=π/302:57View SolutionA particle moves under the action of a force F=20hati + 15hatj along a straight line 3y + alphax =5 , where, alpha is a constant. If the work done by the force F is zero the value of alpha is .
03:24View SolutionThe work done by a force vec(F)=-5hat(k) as its point of application moves from the point (1,1,1) to the origin is equal to ………………… .
03:21View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
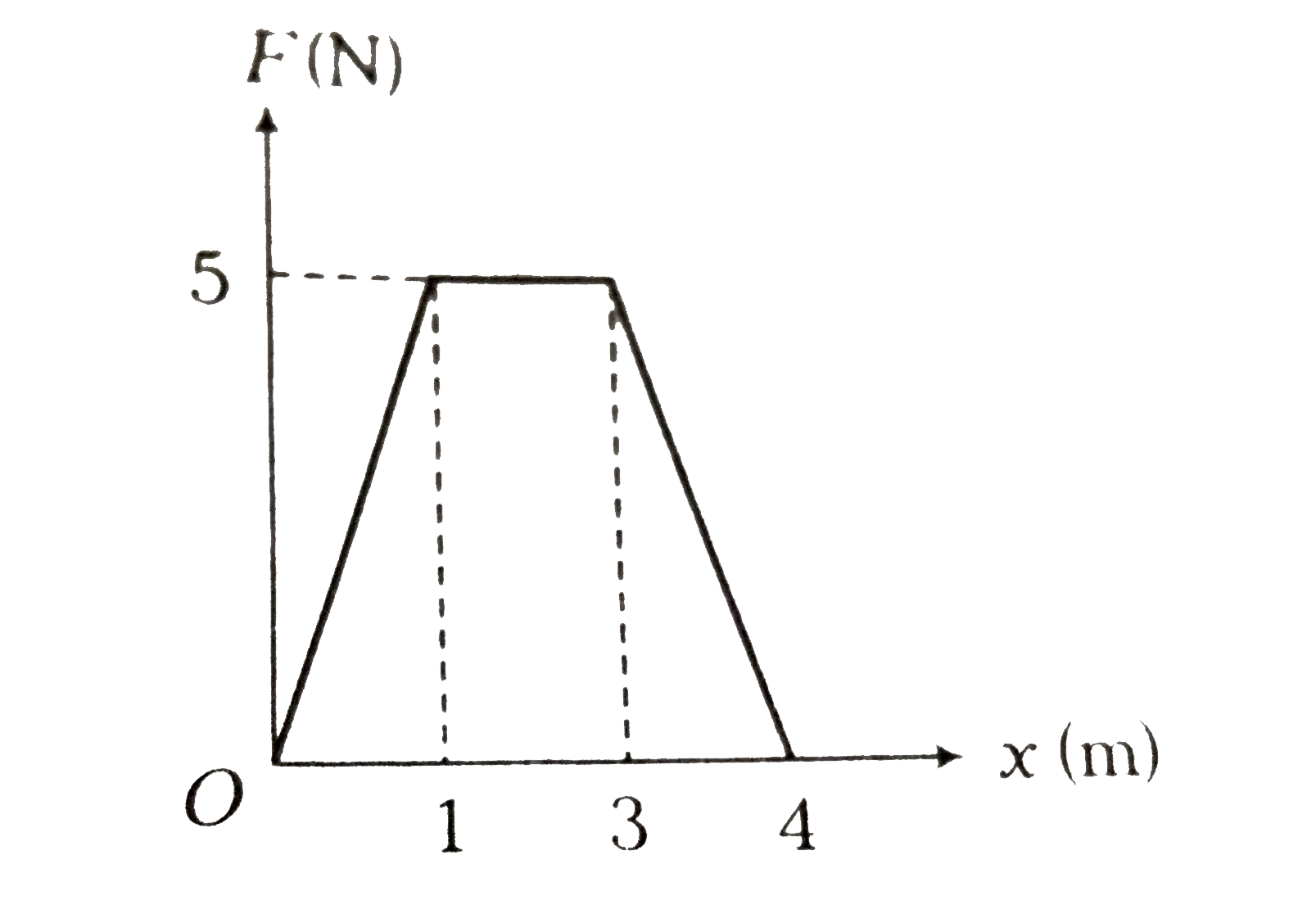 03:21View Solution
03:21View SolutionIf the work done by a force ¯¯¯F=ˆi+mˆj+ˆk in moving the point of application from (1,1,1) to (3,3,3) along a straight is 12 units, then m is
02:40View SolutionFind the work done in moving a particle along a vectors →S=(ˆi−2ˆj+3ˆk)m if applied force is →F=(2ˆi−3ˆj+4ˆk)N.
View SolutionA force →F=k[yˆi+xˆj] where k is a positive constant acts on a particle moving in x-y plane starting from the point (3, 5), the particle is taken along a straight line to (5, 7). The work done by the force is :
03:08View SolutionForce acting on a particle is (2ˆi+3ˆj)N. Work done by the force is zero, when a particle is moved along the line 3y+kx=5. Here the value of k is
02:36View SolutionForce acting on a particle is (2ˆi+3ˆj)N. Work done by the force is zero, when a particle is moved along the line 3y+kx=5. Here the value of k is
01:37View SolutionThe work done by the force ¯¯¯F=a¯i+¯j+¯k in moving a particle from (1,1,1) to (2,2,2) along a straight line is 5 units. Then a =
02:00View SolutionForce acting on a particle is (2ˆi+3ˆj)N. Work done by this force is zero, when a particle is moved along the line 3y+kx=5. Here the value of k is
01:34View Solution

