A : If X is a poisson variate such that P(X=2)=9P(X=4) then variance =2/3
R : The variancen of a poisson variate with parameter λ. Solution in Telugu
Both A and R are true and R is the correct explanation of A
Both A and R are true but R is not correct explanation of A
A is true but R is false
A is false but R is true
The correct Answer is:D
Step by step video, text & image solution for A : If X is a poisson variate such that P(X=2)=9P(X=4) then variance =2//3 R : The variancen of a poisson variate with parameter lambda. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEORETICAL DISTRIBUTIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORETICAL DISTRIBUTIONSEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) CHOOSE THE CORRECT ANSWER FROM THE ALTERNATIVES 1.2.3 OR 4 GIVEN (SET -3)
4 Videos
- THE PLANEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THE PLANEEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET 4
4 Videos
- THEORY OF EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 4
4 Videos
Similar Questions
A random variable X has the following distribution
x1234P(X=x)c2c3c4c
Match the following .
I.c= (a)1II.Mean= (b)0.1III.Variance= (c)3
View SolutionA: The equation of the plane passing through the point (- 1, 2, 4) and parallel to the plane 2x + 3y – 5z +6=0 is 2x + 3y - 5z + 16 = 0.
R: The equation of the plane passing through the point (x1,y1,z1) and parallel to the plane ax + by + cz +d=0 is a(x–x1)+b(y−y1)+c(z−z1)=0
View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.
View SolutionIf X is a Poisson variate such that P(X=0)=P(X=1), then the parameter λ=
View SolutionIf X is a random Poisson variate such that α=P(X=1)=P(X=2) then P(X=4)=
View SolutionIf X is a Poisson variate such that P(X=2)=9P(X=4), then the mean and variance of X are
View SolutionIf X is a Poisson variate such that P(X=2)=9P(X=4)+90P(X=6), then mean of X is
View SolutionIf X is a Poisson variate with P(X=0)=0.8, then the variance of X is
View SolutionIf X is a poisson variate with P(x=0)=0.8 then the variance of x is
View SolutionIf X is a Poisson variate such that P(X=2)=9P(X=4), then the mean and variance of X are
View SolutionIf x is a Poisson variate such that P(x=0)=0.1 ,P(x=2)=0.2 then the parameter λ is
View SolutionFor a poisson variate X, P(X = 2) = P(X = 3) find variance of X.
View SolutionA poisson variate x is such that P(x=2)=9P(x=4)+90.P(x=6) then mean and standard deviation are
View SolutionX is a poisson variate with parameter λ. Then match the following.
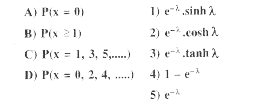
The correct matching is
View SolutionFor a poisson variate X,P(X=2)=P(X=3) find variance of X.
View Solution
