The length of the tangent from a point on the circle x2+y2+4x−6y−12=0 to the circle x2+y2+4x−6y+4=0 is Solution in Telugu
4
12
16
8
The correct Answer is:A
Step by step video, text & image solution for The length of the tangent from a point on the circle x^(2)+y^(2)+4x-6y-12=0 to the circle x^(2)+y^(2)+4x-6y+4=0 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1C(Pole, Polar)107videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1D(Angle Between Circles)49videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1A(Circle)110videos
CIRCLE
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 44videos
BINOMIAL THEOREM
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)5videos
COMPLEX NUMBERS
Similar Questions
The polar of the point (3,4) w.r.t. x2+y2=25 is
03:48View SolutionThe number of common tangents that can be drawn to the circles x2+y2−4x+6y+8=0,x2+y2−10x−6y+14=0
03:39View SolutionThe equation of the circle with centre (3, -2) and radius 3 is
00:57View SolutionA : If the coefficients of 5th, 6th , 7th terms of (1+x)n are in A.P. then n=7or14.
R : If the coefficients of rth, (r+1)th,(r+2)th terms of (1+x)n are in A.P. then n2−(4r+1)n+4r2=2.03:22View SolutionA : If argument of z1=π/3 , argument of z2=π/4 then argument of z1z2 is 7π/12
R : Arg (z1z2)=Argz1+Argz201:56View SolutionTangents are drawn from a point on the circle x2+y2−4x+6y−37=0 to the circle x2+y2−4x+6y−12=0. The angle between the tangents, is
04:22View SolutionThe circles x2+y2−4x−6y−12=0 and x2+y2+4x+6y+4=0
04:27View SolutionThe radius of the circle x2+y2+4x−6y+12=0 is
02:04View SolutionCenter of the circle x2+y2−4x+6y−12=0 is -
07:57View SolutionThe square of the length of tangent from (3, –4) on the circle x2+y2–4x–6y+3=0
02:25View SolutionFind the length of the tangent from any point on the circule
x2+y2−4x+6y−2=0 to the circle x2+y2−4x+6y+7=002:54View Solutionস্পর্শকের দৈর্ঘ্য নির্ণয় করো:
x2+y2−4x+6y−2=0 বৃত্তের ওপর যে-কোনো বিন্দু থেকে x2+y2−4x+6y+7=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য নির্ণয় করো02:45View Solution(−3,9) বিন্দু থেকে x2+y2−4x+6y−12=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য নির্ণয় কর।
01:54View SolutionIf x+y+7=0 is a tangent to the circle x2+y2−4x−6y+k=0 then the point of contact is
06:04View SolutionThe length of the tangent drawn from any point on the circle : x2+y2−4x+2y−4=0 to the circle x2+y2−4x+6y=0 is :
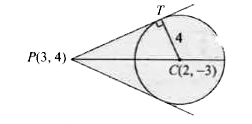
02:40View SolutionFind the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
 02:50View Solution
02:50View Solution

