The polar of three points with respect to a given circle are concurrent, then the three points
are the vertices of an equilateral triangle
are collinear
are coincident
none
The correct Answer is:B
Topper's Solved these Questions
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1D(Angle Between Circles)
49 Videos
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 2(Special Type Questions)
5 Videos
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Exercise 1B(Circle-Line)
142 Videos
- BINOMIAL THEOREMBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos
- COMPLEX NUMBERS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
5 Videos
Similar Questions
Knowledge Check
The chords of contact of tangents from three points A,B,C to the circle x2+y2=a2 are concurrent then the points A, B, C are
AconcyclicBcollinearCvertices of a triangleDnoneIf 25 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, then number of points at which they will intersect are
A300B150C100D250The chord of contact of tangents from three points P, Q, R to the circle x2+y2=c2 are concurrent, then P, Q, R
Aform a triangleBare concyclicCare collinearDnone of these
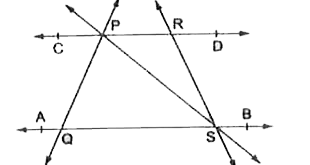
In the adjoining figure , name :
(i)four pairs of intersecting lines
(ii)four collinear points
(iii)three noncollinear points
(iv) three concurrent lines
(v) three lines whose point of intersection is P.
View SolutionThe three concurrent edges of a parallelopiped represent the vectors →a,→b,→c such that [→a→b→c]=V. Then the volume of the parallelopiped whose three concurrent edges are the three diagonals of three faces of the given parallelopiped is
View SolutionThe chords of contact of tangents from three points A,BandC to the circle x2+y2=a2 are concurrent. Then A,BandC will be
View SolutionThe three concurrent edges of a parallelopiped represent the vectors →a,→b,→c such that [→a→b→c]=V. Then the volume of the parallelopiped whose three concurrent edges are the three diagonals of three faces of the given parallelopiped is
View SolutionIf three concurrent edges of a parallelopiped of volume V represent vectors →a,→b,→c then the volume of the parallelopiped whose three concurrent edges are the three concurrent diagonals of the three faces of the given parallelopiped is
View Solution
