For the circle C with the equation x2+y2−16x−12y+64=0 match the list-I with the list-II given below: 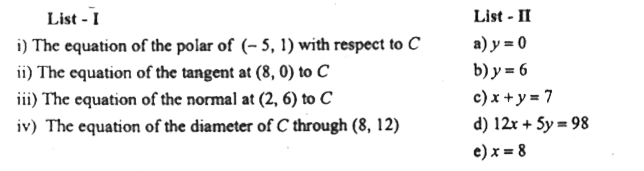
I) d. ii). b, iii). a, iv). c
I) d. ii). a, iii). b, iv). e
I) c. ii). d, iii). a, iv). b
I) c. ii). e, iii). b, iv). a
The correct Answer is:C
Topper's Solved these Questions
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Set 4
4 Videos
- CIRCLEBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - CIRCLEEXERCISE - Set 2
4 Videos
- BINOMIAL THEOREMBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos
- COMPLEX NUMBERS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - COMPLEX NUMBERS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
5 Videos
Similar Questions
If α and β are the zeroes of the polynomial 2x2−4x+5 then match the value of List-I with that of List-II.
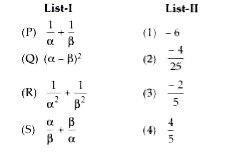
View Solution(i) Find the equation of a circle , which is concentric with the circle x2+y2−6x+12y+15=0 and of double its radius.
(ii) Find the equation of a circle , which is concentric with the circle x2+y2−2x−4y+1=0 and whose radius is 5.
(iii) Find the equation of the cricle concentric with x2+y2−4x−6y−3=0 and which touches the y-axis.
(iv) find the equation of a circle passing through the centre of the circle x2+y2+8x+10y−7=0 and concentric with the circle
2x2+2y2−8x−12y−9=0.
(v) Find the equation of the circle concentric with the circle x2+y2+4x−8y−6=0 and having radius double of its radius.
View Solution
Knowledge Check
The equation 16x2−3y2−32x−12y−44=0 represents a hyperbola, which one of the following is /are correct
Atransverse axis is 4√3Bconjugate axis is 4Ceccentricity is √19√3.Dcentre is (−1,2)The equation 16x2−3y2−32x−12y−44=0 represents a hyperbola, which one of the following is /are correct
Athe length of whose transverse axis is 4√3Bthe length of whose conjugate axis is 4Cwhose centre is (-1,2)Dwhose eccentricity is √19/3Tangent to the curve y=x2+6 at a point P(1, 7) touches the circle x2+y2+16x+12y+c=0 at a point Q. Then the coordinates of Q are
A(−6,−11)B(−9,−13)C(−10,−15)D(−6,−7)
Let x and y be positive real numbers such that y3+y≤x−x3 . Then match the following list -I with List- II Where [.] is greatest integer function.
List - I List - II(P)[x1x−y1y](1)−1(Q)[x1x−1](2) 0(R) [3−(1−x)2](3) 1(s) [x2−y2+1](4)2
View SolutionConsider the parabola y2=12x and match the following lists :

View SolutionFind the equation of the image of the circle x2+y2+8x−16y+64=0 in the line mirror x=0.
View SolutionIf the tangent at (1,7) to curve x2=y−6 touches the circle x2+y2+16x+12y+c=0 then the value of c is
View SolutionIf the tangent at (1,7) to curve x2=y−6 touches the circle x2+y2+16x+12y+c=0 then the value of c is
View Solution
