If c, d, and e are consecutive iintegers, what is cde?
To solve the problem, we need to determine the product of three consecutive integers c, d, and e and whether this product is even or odd.
1. Understanding Consecutive Integers:
- Consecutive integers are numbers that follow one another in order. For example, if c is an integer, then d=c+1 and e=c+2. Thus, we can express the three consecutive integers as c, c+1, and c+2.
2. Identifying Even and Odd:
- Among any three consecutive integers, at least one of them must be even. This is because integers alternate between odd and even. Therefore, in any set of three consecutive integers, there will always be one even integer.
3. Calculating the Product:
- The product of these integers can be expressed as:
c×d×e=c×(c+1)×(c+2)
4. Analyzing the Product:
- Since one of the integers c, d, or e is guaranteed to be even, the product of any integer with an even number will always yield an even result. Thus:
c×d×e is even.
5. Conclusion:
- Therefore, the product cde of three consecutive integers c, d, and e is always even.
Final Answer:
The product cde is even.
---
- Consecutive integers are numbers that follow one another in order. For example, if c is an integer, then d=c+1 and e=c+2. Thus, we can express the three consecutive integers as c, c+1, and c+2.
- Among any three consecutive integers, at least one of them must be even. This is because integers alternate between odd and even. Therefore, in any set of three consecutive integers, there will always be one even integer.
- The product of these integers can be expressed as:
c×d×e=c×(c+1)×(c+2)
- Since one of the integers c, d, or e is guaranteed to be even, the product of any integer with an even number will always yield an even result. Thus:
c×d×e is even.
- Therefore, the product cde of three consecutive integers c, d, and e is always even.
The product cde is even.
Similar Questions
Knowledge Check
- Question 1 - Select One
Suppose that the average (arithmetic mean) of a, b and c is h, the average of b, c, and d is j, and the average of d and e is k.
What is the average of a and e?Ah−j+kB3h+3j−2k2C3h−3j+2k2D3h−3j+2k5
A, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionA,B,C,D,E, and F are conducting plates each of area A, and any two consecutive plates are separated by a distance d, The energy in system after the switch S is closed is
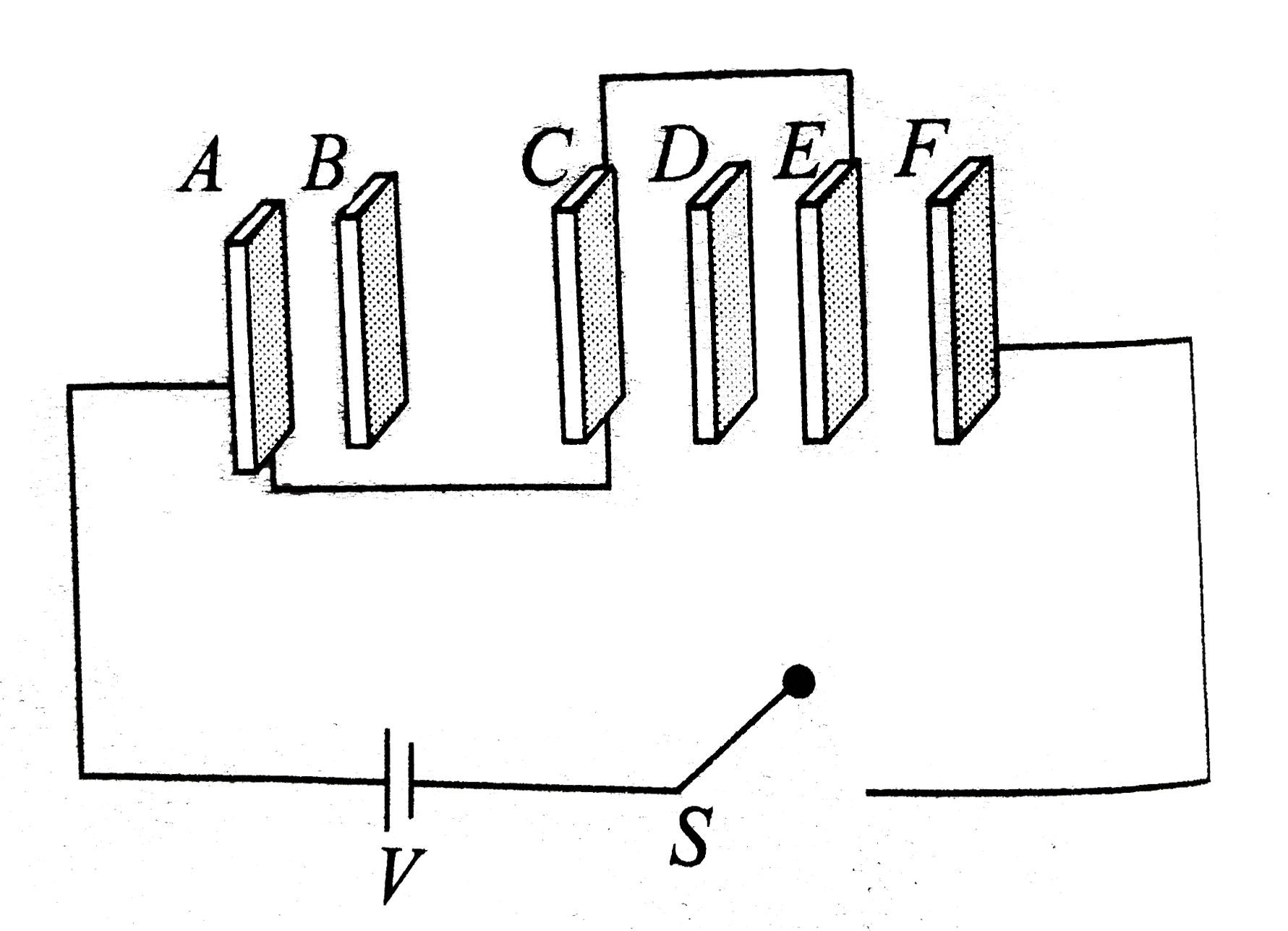 .View Solution
.View SolutionIn ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View Solutionif a,b,c and d are the coefficient of four consecutive terms in the expansion of (1+x)n then aa+b+cc+d=?
View SolutionIn Figure, AD and BE are respectively perpendiculars to BC and AC . Show that: (i)△ADC~△BEC (ii)CA×CE=CB×CD (iii)△ABC~△DEC (iv)CD×AB=CA×DE
View SolutionIf →a, →b are the vectors forming consecutive sides of a regular of a regular hexagon ABCDEF, then the vecrtor representing side CD is
a.→a+→b b. →a−→b c. →b−→a d. −(→a+→b)View SolutionIf a,b,c,d,e are five numbers such that a,b,c are in A.P., b,c,d are in G.P. and c,d, e ar in H.P. prove that a,c,e are in G.P.
View Solution

