If ab>0, which of the following must be negative ?
a+b
|a|+b
b−a
−ab
The correct Answer is:D
To solve the problem, we need to analyze the given condition ab>0 and determine which of the provided options must be negative.
1. Understanding the Condition:
The condition ab>0 indicates that the product of a and b is positive. This can occur in two scenarios:
- Case 1: Both a and b are positive (a>0 and b>0).
- Case 2: Both a and b are negative (a<0 and b<0).
2. Analyzing Each Option:
We need to check each option to see if it must be negative under both cases.
- Option A: a+b:
- In Case 1 (both positive): a+b>0 (not negative).
- In Case 2 (both negative): a+b<0 (negative).
- Conclusion: Not necessarily negative.
- Option B: |a|+|b|:
- In Case 1: |a|+|b|>0 (not negative).
- In Case 2: |a|+|b|>0 (not negative).
- Conclusion: Not necessarily negative.
- Option C: b−a:
- In Case 1: If b<a, b−a<0 (negative), but if b>a, b−a>0 (not negative).
- In Case 2: If both are negative, the result can vary based on their values.
- Conclusion: Not necessarily negative.
- Option D: −ab:
- In Case 1: −ab<0 (negative).
- In Case 2: −ab<0 (negative).
- Conclusion: Must be negative.
3. Final Conclusion:
The only option that must be negative in both cases is Option D: −ab.
Final Answer:
Option D must be negative.
---
The condition ab>0 indicates that the product of a and b is positive. This can occur in two scenarios:
- Case 1: Both a and b are positive (a>0 and b>0).
- Case 2: Both a and b are negative (a<0 and b<0).
We need to check each option to see if it must be negative under both cases.
- In Case 1 (both positive): a+b>0 (not negative).
- In Case 2 (both negative): a+b<0 (negative).
- Conclusion: Not necessarily negative.
- In Case 1: |a|+|b|>0 (not negative).
- In Case 2: |a|+|b|>0 (not negative).
- Conclusion: Not necessarily negative.
- In Case 1: If b<a, b−a<0 (negative), but if b>a, b−a>0 (not negative).
- In Case 2: If both are negative, the result can vary based on their values.
- Conclusion: Not necessarily negative.
- In Case 1: −ab<0 (negative).
- In Case 2: −ab<0 (negative).
- Conclusion: Must be negative.
The only option that must be negative in both cases is Option D: −ab.
Option D must be negative.
Similar Questions
Knowledge Check
- Question 1 - Select One
If B3A<0andA>0 which of the following must be negative?
AABBB2ACB4DAB2 - Question 2 - Select One
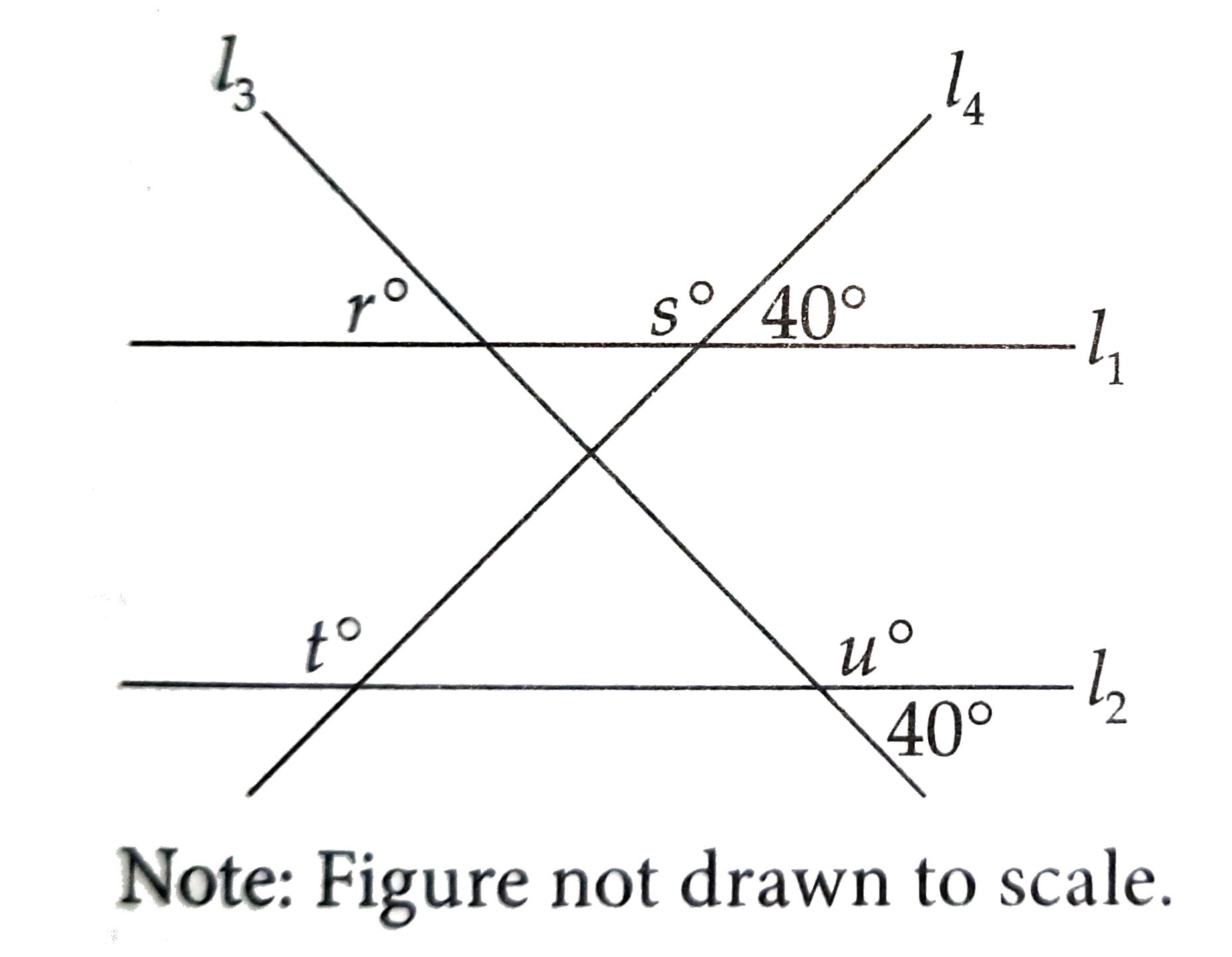
Which of the following must be true?Al1∣∣l2Bl3 bisects l4Cs=tDu=140∘ - Question 3 - Select One or More
If r is negative, which of the following must also be negative?
Ar2Br3Cr4Dr2⋅r3
If a+b>0 and c+d>0, which of the following must be true ?
View SolutionIf ab<0,a>b,andb>−b, which of the following must be true?
View SolutionIf ln (xy)<0, which of the following must be true ?
View SolutionIf xy<0, which of the following must be true?
I.x+y=0
II. 2x−2y<0
III. x2+y2>0View SolutionIF x+y=0, which of the following must be equivalent to x-y?
View Solution

