A magician has five animals in his magic hat : 3 doves and 2 rabbits. If he pulls two animals out of the hat at random, what is the chance that he will have a matched pair?
50%
40%
60%
30%
The correct Answer is:40%
To solve the problem of finding the probability that the magician pulls out a matched pair of animals (either both doves or both rabbits), we can follow these steps:
Step 1: Identify the total number of animals
The magician has a total of 5 animals: 3 doves and 2 rabbits.
Step 2: Calculate the total number of ways to choose 2 animals from 5
The total number of ways to choose 2 animals from 5 can be calculated using the combination formula:
Total ways=(nr)=n!r!(n−r)!
where n is the total number of animals and r is the number of animals to choose.
For our case:
Total ways=(52)=5!2!(5−2)!=5×42×1=10
Step 3: Calculate the number of ways to pick a matched pair of rabbits
To find the number of ways to pick 2 rabbits from the 2 available:
Ways to choose 2 rabbits=(22)=1
Step 4: Calculate the number of ways to pick a matched pair of doves
To find the number of ways to pick 2 doves from the 3 available:
Ways to choose 2 doves=(32)=3!2!(3−2)!=3×22×1=3
Step 5: Calculate the total number of ways to get a matched pair
The total number of ways to get a matched pair (either both rabbits or both doves) is:
Total matched pairs=Ways to choose 2 rabbits+Ways to choose 2 doves=1+3=4
Step 6: Calculate the probability of getting a matched pair
The probability of getting a matched pair is given by the ratio of the number of favorable outcomes to the total outcomes:
P(matched pair)=Total matched pairsTotal ways=410=25
Final Answer
The probability that the magician will pull out a matched pair of animals is 25 or 0.4.
---
The magician has a total of 5 animals: 3 doves and 2 rabbits.
The total number of ways to choose 2 animals from 5 can be calculated using the combination formula:
Total ways=(nr)=n!r!(n−r)!
where n is the total number of animals and r is the number of animals to choose.
Total ways=(52)=5!2!(5−2)!=5×42×1=10
To find the number of ways to pick 2 rabbits from the 2 available:
Ways to choose 2 rabbits=(22)=1
To find the number of ways to pick 2 doves from the 3 available:
Ways to choose 2 doves=(32)=3!2!(3−2)!=3×22×1=3
The total number of ways to get a matched pair (either both rabbits or both doves) is:
Total matched pairs=Ways to choose 2 rabbits+Ways to choose 2 doves=1+3=4
The probability of getting a matched pair is given by the ratio of the number of favorable outcomes to the total outcomes:
P(matched pair)=Total matched pairsTotal ways=410=25
The probability that the magician will pull out a matched pair of animals is 25 or 0.4.
Similar Questions
Renee has a bag of 6 candies, 4 of which are sweet and 2 of which are sour. Jack picks two candies simultaneously and at random. What is the chance that exactly one of the candies he has picked is sour?
View SolutionIn a bag of marbles, there are 3 red, 2 white, and 5 blue marbles. If Kia takes 2 marbles out of the bag, what is the probability that he will have 1 white and 1 blue marbole?
(Assume that Kia does not replace the marbles in the beg.)View Solution
Knowledge Check
- Question 1 - Select One
Thomas and Jonelle are playing darts in their garage using the board with the point value for each region shown below. The radius of the outside circle is 10 inches, and each of the other circles has a radius 2 inches smaller than the next larger circle. All of the circles have the same center. Thomas has only 1 dart left to throw and needs at least 30 points to win the game. Assuming that his last dart hits at a random point within a single region on the board, what is the percent chance that Thomas will win the game?
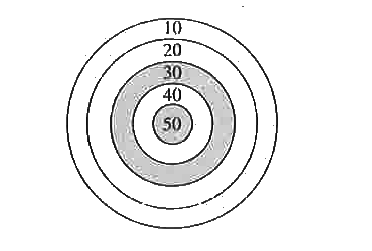 A36%B0.3C0.16D0.09
A36%B0.3C0.16D0.09 - Question 2 - Select One
John participated in a game where each participant was asked to pick up six cards from a box without looking at the cards. The participant with the highest total would be declared the winner. Each card had a numerical value from one to a hundred written on it. John's average in the first four cards came out to be 83.What is the lowest he can get in the sixth draw so that he still has a chance of taking his overall average to at least 88 ?
A100B98C96D92
A test for detection of a particular disease is not fool proof. The test will correctly detect the disease 90% of the time, but will incorrectly detect the disease 1% of the time. For a large population of which an estimated 0.2% have the disease, a person is selected at random, given the test, and tod that he has the disease. What are the chances that the person actually have the disease?
View SolutionA room has 3 lamps . From a collection of 10 light bulbs of which 6 are no good , a person selects 3 at random and puts them in a socket . What is the probability , that he will have light ?
View Solution105 goats, 140 donkeys and 175 cows have to be taken across a river. There is only one boat which will have to make many trips in order to do so. The lazy boatman has his own conditions for transporting them. He insists that he will take the same number of animals in every trip and they have to be of the same kind. He will naturally like to take the largest possible number each time. Can you tell how many animals went in each trip?
View SolutionA florist has 2 azaleas, 3 buttercups, and 4 petunias. She puts two flowers together a random in a bouquet. However, the coustomer cells and says tha she does not want two of the same flower. What is the probability that the florist does not have to change two bouquet?
View SolutionProfessor Malingowski, a chemist and teacher at to communite college, is organizing his graduated cylinders in the hopes of keeping his office tidy and setting a good example for his students. He has beakers with diameters, in inches, of 12,34,45,1 and 54.
Professor Malingowski notices one additional cylinder lying on the ground, and can recall certain facts about it, but not its actual diameter. If he knows that the value of the additional graduated cylinder's diameter ,x, will not create any modes and will make the mean of the set equal to 56, what is the value of the additional cylinder's diameter?View SolutionTwo particles of equal mass have velocities →v1=2ˆi=m/s−1 and →v2=2ˆjm/s−1. First particle has an acceleration →a1=(3ˆi+3ˆj)ms−2 while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of.
View Solution

