For all real numbers x, let the function g be defined by , wher p, h and k are constants with . Which of the following CANNOT be true?
The correct Answer is:C
To solve the problem, we need to analyze the function g(x)=p(x−h)2+k, where p,h,k are constants with p>0 and k>0. We want to determine which of the provided options cannot be true.
1. Understanding the Function:
The function g(x)=p(x−h)2+k is a quadratic function that opens upwards because p>0. The term (x−h)2 is always non-negative (i.e., (x−h)2≥0), which means g(x) will always be at least k.
2. Finding the Minimum Value:
Since (x−h)2 is minimized at x=h, the minimum value of g(x) occurs at:
g(h)=p(0)+k=k
Given that k>0, the minimum value of g(x) is k, which is positive. Therefore, g(x) can never be less than k and is always positive.
3. Analyzing the Options:
Now we will analyze each option to see if it can be true given that g(x) is always positive.
- Option 1: g(7)=−h
- Since h can be any real number, −h can be positive or negative. Therefore, this option can potentially be true depending on the value of h.
- Option 2: g(7)=2
- This is a positive value. Since g(x) can take positive values, this option can be true.
- Option 3: g(0)=−2
- This is a negative value. Since we established that g(x) is always positive, this option cannot be true.
- Option 4: g(0)=2
- This is a positive value. Therefore, this option can be true.
4. Conclusion:
The only option that cannot be true is Option 3: g(0)=−2.
Final Answer:
The option that cannot be true is: Option 3: g(0)=−2.
The function g(x)=p(x−h)2+k is a quadratic function that opens upwards because p>0. The term (x−h)2 is always non-negative (i.e., (x−h)2≥0), which means g(x) will always be at least k.
Since (x−h)2 is minimized at x=h, the minimum value of g(x) occurs at:
g(h)=p(0)+k=k
Given that k>0, the minimum value of g(x) is k, which is positive. Therefore, g(x) can never be less than k and is always positive.
Now we will analyze each option to see if it can be true given that g(x) is always positive.
- Since h can be any real number, −h can be positive or negative. Therefore, this option can potentially be true depending on the value of h.
- This is a positive value. Since g(x) can take positive values, this option can be true.
- This is a negative value. Since we established that g(x) is always positive, this option cannot be true.
- This is a positive value. Therefore, this option can be true.
The only option that cannot be true is Option 3: g(0)=−2.
The option that cannot be true is: Option 3: g(0)=−2.
Similar Questions
If f be a function defined as f(x) = p for each x∈R, where p is a real number, then f is called
View SolutionLet A and B be two fixed points and P, another point in the plane, moves in such a way that k1PA+k2PB=k3, where k1, k2 and k3 are real constants. The locus of P is
Which one of the above is not true ?View Solution
Knowledge Check
- Question 1 - Select One
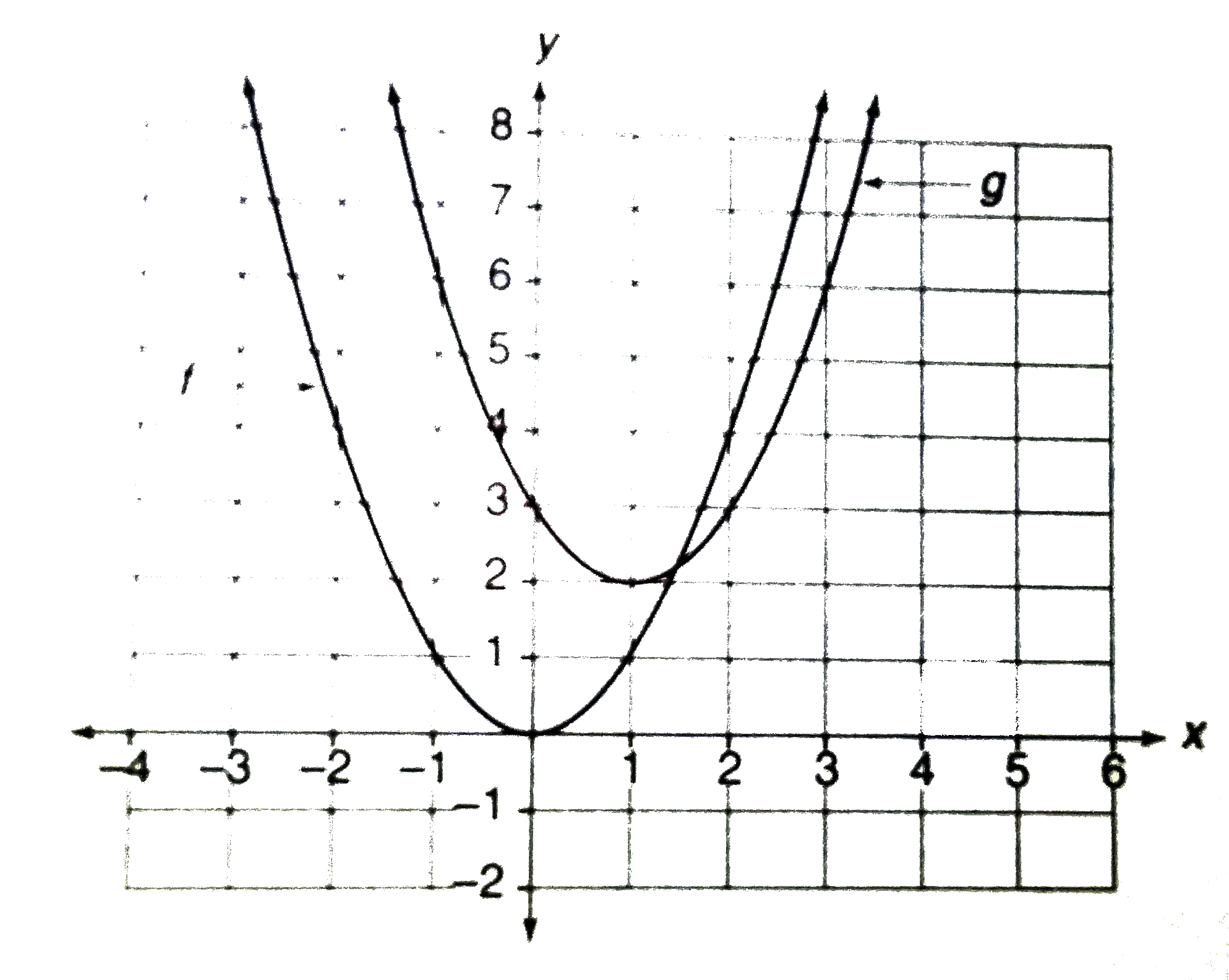
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?A−3B−2C−1D1 - Question 2 - Select One
If (x+p) is a factor of both x2+16x+64and4x2+37x+k, where p and k are nonzero integer constants, what could be the value of k?
A9B24C40D63 - Question 3 - Select One
At constant temperature , the equilibrium constant (KP) for the decomposition reaction
N2O4⇔2NO2, is expressed by Kp=(4x2p)(1−x2)
where p= pressure ,x = extent of decomposition .which one of the following statements is true?AKp increase with increase of pBKp increases with increase of xCKp increases with decrease of xDKp remains constant with change in P and X.
Let function f be defined as f:R+→R+ and function g is defined as g:R+→R+. Functions f and g are continuous in their domain. Suppose, the function h(x)=limn→∞xnf(x)+x2xn+g(x),x>0. If h(x) is continuous in its domain,thenf(1).g(1) is equal to (a) 2 (b) 1 (c) 12 (d) 0
View SolutionLet g:R→(0,π3) be defined by g(x)=cos−1(x2−k1+x2) . Then find the possible values of k for which g is a surjective function.
View SolutionThe polynomial function p is defined by p(x)=4x3+bx2+41x+12, where b is a constant. When graphed on a standard coordinate plane, p intersects the x-axis at (−0.25,0),(3,0)and(k,0). What is the value of b?
View SolutionConsider the exponential equation y=p(x+1)K, where K and p are positive real constants and x is a positive real number. The value of y decreases as the value of x increases if and only if which of the following statements about p is true ?
View Solutionx2−k2x=2p
In the quadratic equation above, kandp are constants. What are the solutions for x ?View Solution

