k=a−b+12,k=b−c−17,k=c−a+11
In the system of equations above, what is the value of k?
The correct Answer is:2
To solve the system of equations given by:
1. k=a−b+12
2. k=b−c−17
3. k=c−a+11
we will follow these steps:
Step 1: Write down the equations
We have three equations:
- k=a−b+12 (Equation 1)
- k=b−c−17 (Equation 2)
- k=c−a+11 (Equation 3)
Step 2: Set up the equation for summation
We can add all three equations together:
k+k+k=(a−b+12)+(b−c−17)+(c−a+11)
Step 3: Simplify the left side
The left side simplifies to:
3k
Step 4: Simplify the right side
Now, let's simplify the right side:
- Combine like terms:
(a−b+b−c+c−a)+(12−17+11)
- The terms a, −b, b, −c, c, and −a cancel out:
0+(12−17+11)
- Now calculate the constants:
12−17=−5
−5+11=6
So, the right side simplifies to:
6
Step 5: Set the equations equal
Now we have:
3k=6
Step 6: Solve for k
To find k, divide both sides by 3:
k=63=2
Final Answer
Thus, the value of k is:
2
---
2. k=b−c−17
3. k=c−a+11
We have three equations:
- k=a−b+12 (Equation 1)
- k=b−c−17 (Equation 2)
- k=c−a+11 (Equation 3)
We can add all three equations together:
k+k+k=(a−b+12)+(b−c−17)+(c−a+11)
The left side simplifies to:
3k
Now, let's simplify the right side:
- Combine like terms:
(a−b+b−c+c−a)+(12−17+11)
- The terms a, −b, b, −c, c, and −a cancel out:
0+(12−17+11)
- Now calculate the constants:
12−17=−5
−5+11=6
So, the right side simplifies to:
6
Now we have:
3k=6
To find k, divide both sides by 3:
k=63=2
Thus, the value of k is:
2
Similar Questions
Knowledge Check
{5x−3y=106y=kx−42
In the system of linear equations above, k represents a constant. If the system of equations has no solution, what is the value of 2k?A52B5C10D20√2k2+17−x=0
If k gt 0 and x = 7 in the equation above, what is the value of k ?A2B3C4D5x+7y=−10
3x−4y=k
In the system of equation above,k is a constant. IF (a,b) is the solution to the system, what is the value of a, in terms of k?A−k−3025B3k+1025C6k−825D7k−4025
(k−1)x+13y=4
k(x+2y)=7
In the system of linear equations above, k is a constant. If the system has no system, what is the value of k?
View Solution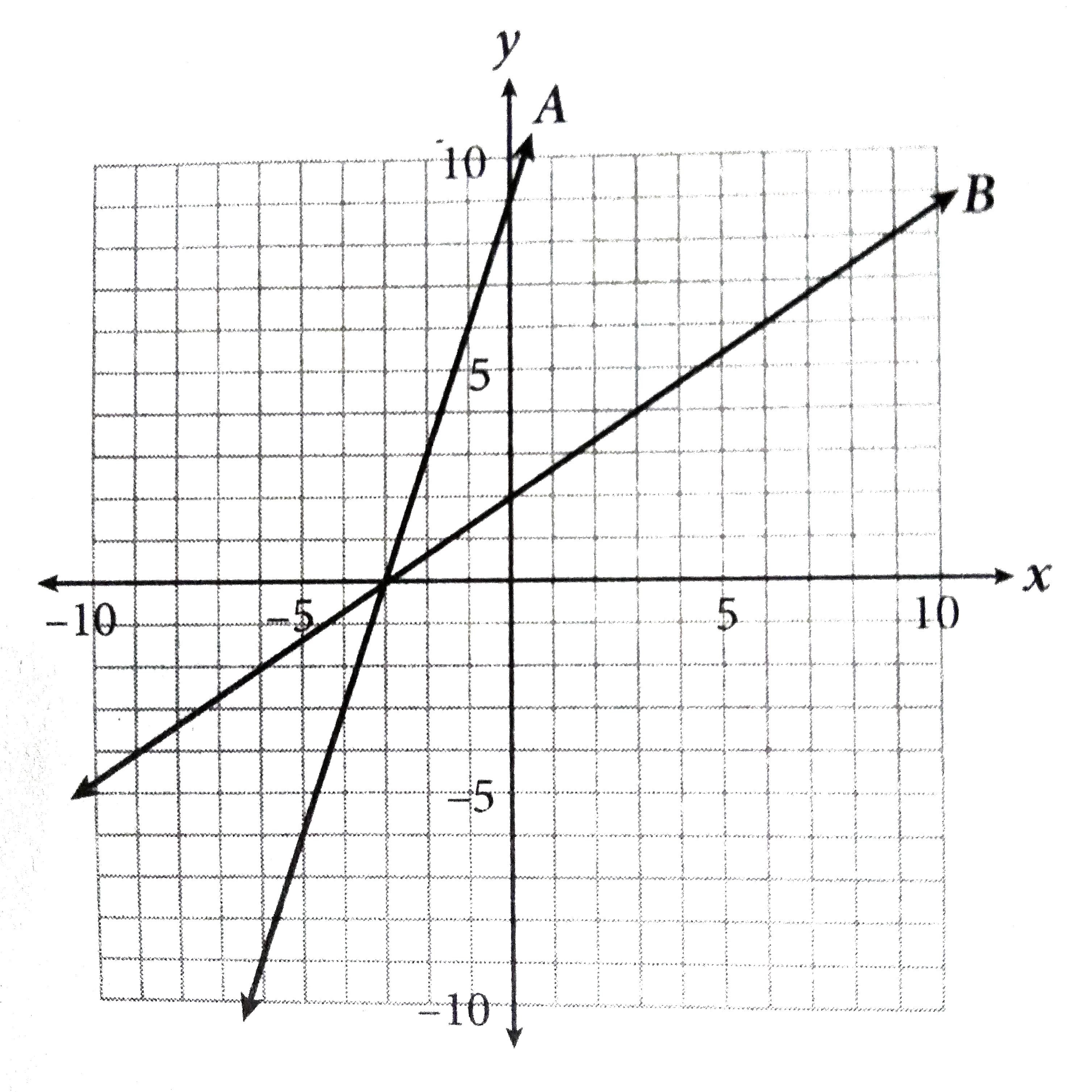
If the equation of line A shown on the graph is given by y=mx+b, and the equation of line B is given by y=k(mx+b), what is the value of k?
View Solution{34x−12y=12kx−2y=22
If the system of linear equations above has no solution, and k is a constant, what is the value of k?
View Solutionkx−3y=4
4x−5y=7
In the system of equations above, k is a constant and x and y are variables. For what value of k will the system of equations have no solution?
View Solution4x+6y=12
y=80−kx
For what value of k does the system of equation above have no solution?
View Solution