A block is sliding down a ramp that drops 3 centimeters in elevation for every 5 centimeters along the length of the ramp. The top of the ramp, where the back edge of the block is initally placed, is at 60 centimeters down the ramp. What is the elevation of the ramp, in centimeters, at the point where the back of the block passes t seconds after being released?
60−35t
60−3t
60−6t
60−9t
The correct Answer is:C
Similar Questions
A block of wood loses 100 J of gravitational potential energy as it slides down a ramp. If it has 90 J of kinetic energy at the bottom of the ramp, what can you conclude ?
View Solution(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
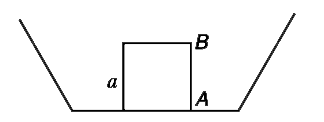
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
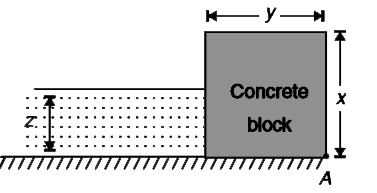
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
View Solution
Knowledge Check
A block of mass m slides with constant speed down a ramp whose incline angle is θ. If F1 is the magnitude of the gravitational force acting parallel to the ramp and F2 is the magnitude of the normal force acting on the block, what is the value of F1/F2?
Am tan θBm cot θC1Dtan θThe blocks are on frictionless inclined ramp and connected by a massless cord. The cord passes over an ideal pully. [g=10m/s2]
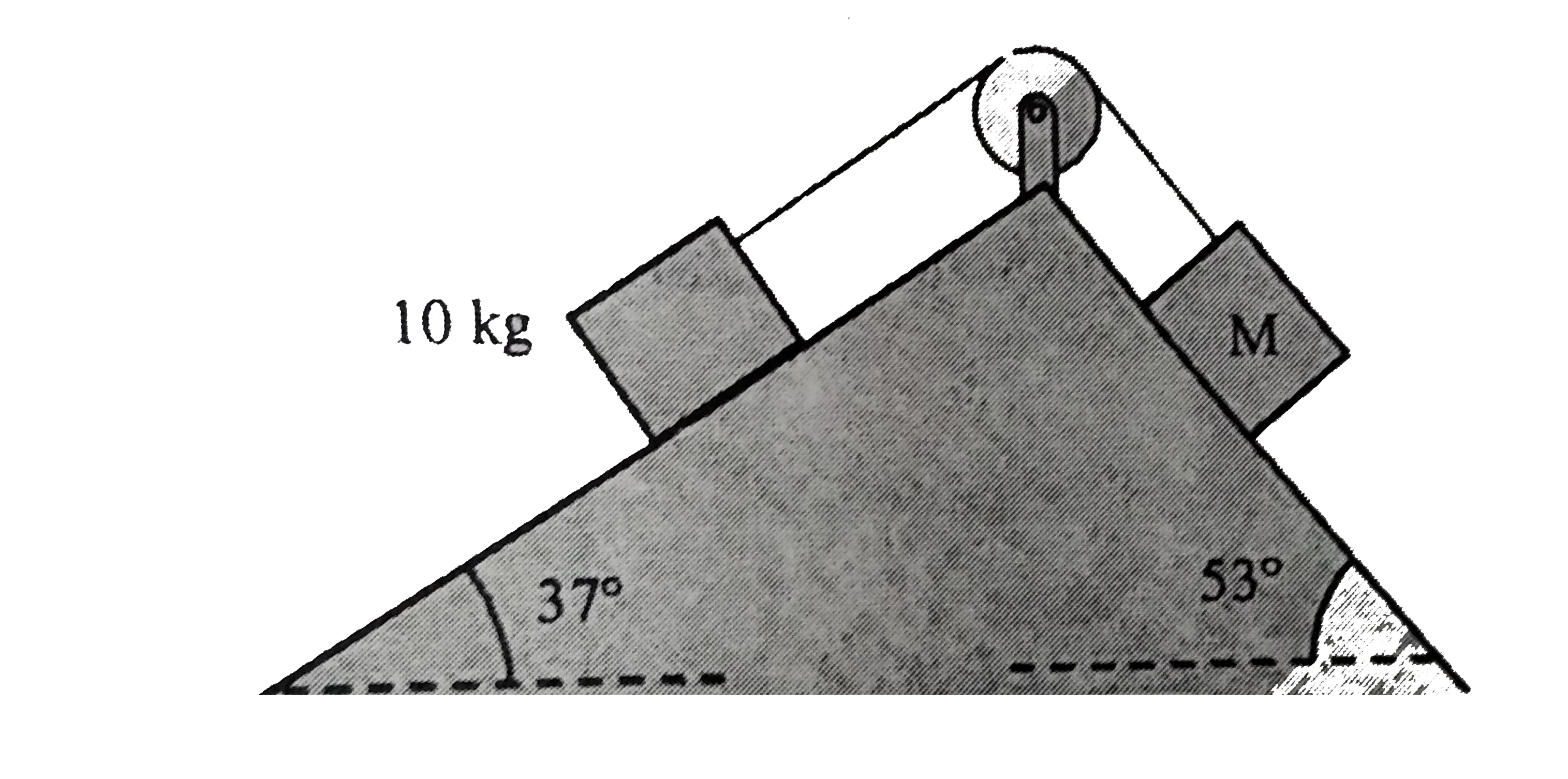
When to 10 kg block slides down the ramp with acceleration of 2m/s2 tension in the crod is closest to :-A80 NB60 NC40 ND30 NA block is attached to a horizontal spring and oscillates back and forth on f frictionless horizontal surface at a frequency of 3.00Hz. The amplitude of the motion is 5.08×10−2m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits?
A5.08×10−2m,4.24HzB3.59×10−2m,4.24HzC2.54×10−2m,3.00HzD3.59×10−2m,6.00Hz
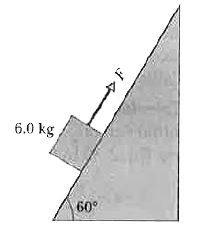
Figure 6-28 shows a 6.0 kg block on a 60∘ ramp with a coefficient of static friction of 0.60. A force →F is applied up the ramp. What magnitude of that force puts the block on the verge of sliding down the ramp? 6.0 kg
View SolutionA particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?

View SolutionA uniform hoop, disk, and sphere, with the same mass M and same radius R, are released simultaneously from rest at the top of a ramp of length L = 2.5 m and angle θ=12∘ with the horizontal. The objects roll smoothly down the ramp.
What is vcom for each object at the bottom of the ramp?
View SolutionThe blocks are on frictionless inclined ramp and connected by a massless cord. The cord passes over an ideal pully. [g=10m/s2]

When to 10 kg block slides down the ramp with acceleration of 2m/s2 tension in the crod is closest to :-
View SolutionA crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery, the center of mass of the crate and its contents is located 0.30 m above the crate's geometrical center. The crate rests on a ramp that makes an angle θ with the horizontal. As θ is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction between ramp and crate is 0.30, (a) does the crate tip or slide and (b) at what angle θ does this occur? If μs=0.70, (c) does the crate tip or slide and (d) at what angle θ does this occur? (Hint: At the onset of tipping, where is the normal force located?)
View Solution
