If a,h, and k are nonzero constants, and the parabola with equation y=a(x−h)2+k, in the xy-plane, passes through the point (h,5) and (0,2) , which of the following must be true ?
h2=−3a
a2=−3h
a=−3h
ah=−3
The correct Answer is:A
To solve the problem, we need to determine the values of the constants a, h, and k based on the given points that the parabola passes through: (h,5) and (0,2). We will use the equation of the parabola, which is given by:
y=a(x−h)2+k
Step 1: Substitute the first point (h,5)
Since the point (h,5) lies on the parabola, we substitute x=h and y=5 into the equation:
5=a(h−h)2+k
This simplifies to:
5=a(0)2+k
Thus, we have:
5=k(Equation 1)
Step 2: Substitute the second point (0,2)
Next, we substitute the second point (0,2) into the equation of the parabola. Here, we set x=0 and y=2:
2=a(0−h)2+k
This simplifies to:
2=a(−h)2+k
Since (−h)2=h2, we can rewrite it as:
2=ah2+k
Step 3: Substitute k from Equation 1
Now, we substitute k=5 from Equation 1 into the equation we derived from the second point:
2=ah2+5
Step 4: Solve for a
Now, we can isolate a:
2−5=ah2
This simplifies to:
−3=ah2
Rearranging gives us:
a=−3h2(Equation 2)
Conclusion
From our calculations, we have determined that k=5 and a=−3h2.
Final Result
The relationships we found must hold true for the constants a, h, and k given the points through which the parabola passes.
Similar Questions
Knowledge Check
Which of the following is an equation of the line in the xy - plane that passes through the point (0,−7) and is perpendicular of the line y=−6x+2?
Ay=−6x+7By=−6x+14Cy=−16x+6Dy=16x−7Which of the following is the graph of the equation y = 2x − 5 in the xy-plane?
A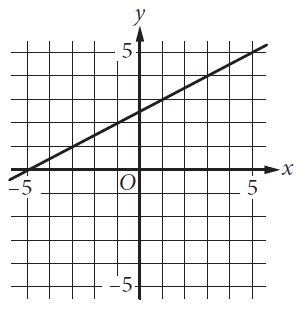 B
B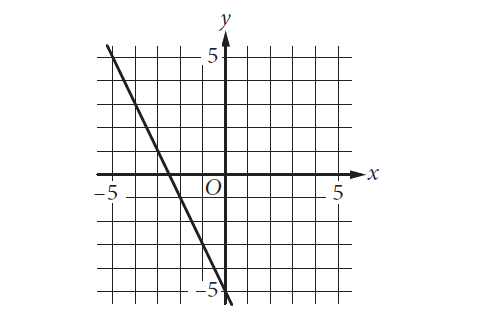 C
C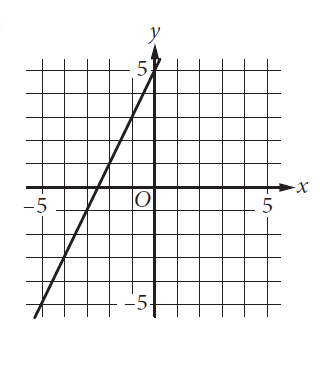 D
D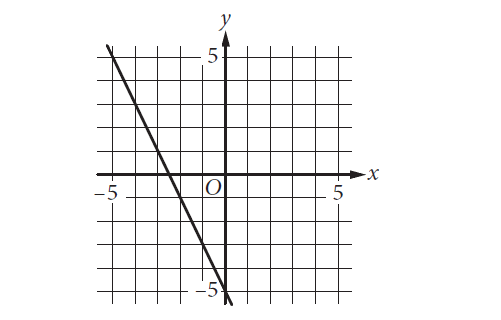
y=a(x−2)(x+4)
In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c,d) . Which of the following is equal to d ?A−9aB−8aC−5aD−2a
Find the equation of tangents of the parabola y2=12x, which passes through the point (2, 5).
View SolutionFind the equation of tangents of the parabola y2=12x, which passes through the point (2, 5).
View Solutiony = f(x) which has differential equation y(2xy+ex)dx−exdy=0 passing through the point (0,1). Then which of the following is/are true about the function?
View SolutionThe line, represented by the equation 3x−8y=2, passes through the point (k, 2). Find the value of k.
View SolutionFind the equation of the circle whose centre is (h,k) and which passes through the point (p,q).
View Solution
