If a3+a2−a−1=0, then which one of the following could be the value of a?
0
1
2
3
The correct Answer is:1
To solve the equation a3+a2−a−1=0, we can follow these steps:
Step 1: Group the terms
We start with the equation:
a3+a2−a−1=0
We can group the terms as follows:
(a3+a2)+(−a−1)=0
Step 2: Factor by grouping
Next, we can factor out common terms from each group:
a2(a+1)−1(a+1)=0
Now, we can factor out (a+1):
(a2−1)(a+1)=0
Step 3: Further factor the quadratic
The expression a2−1 can be factored further using the difference of squares:
(a−1)(a+1)(a+1)=0
Step 4: Set each factor to zero
Now, we set each factor equal to zero:
1. a−1=0 → a=1
2. a+1=0 → a=−1
Step 5: List the possible values
The possible values for a are:
a=1ora=−1
Conclusion
From the given options, the value of a that satisfies the equation is a=1.
Final Answer
Thus, the correct answer is option b: a=1.
---
We start with the equation:
a3+a2−a−1=0
We can group the terms as follows:
(a3+a2)+(−a−1)=0
Next, we can factor out common terms from each group:
a2(a+1)−1(a+1)=0
Now, we can factor out (a+1):
(a2−1)(a+1)=0
The expression a2−1 can be factored further using the difference of squares:
(a−1)(a+1)(a+1)=0
Now, we set each factor equal to zero:
1. a−1=0 → a=1
2. a+1=0 → a=−1
The possible values for a are:
a=1ora=−1
From the given options, the value of a that satisfies the equation is a=1.
Thus, the correct answer is option b: a=1.
Similar Questions
Knowledge Check
Use the method of plugging In to solve the following problem.
If x2+4x+3 is odd, then which one of the following could be the value of x?A3B5C9D16From the figure, which of the following could be the value of b?
 A20B40C50D70
A20B40C50D70If 2x=2y+1, then which of the following could be true?
Ax>yBx<yCx=yD9x+12y=36
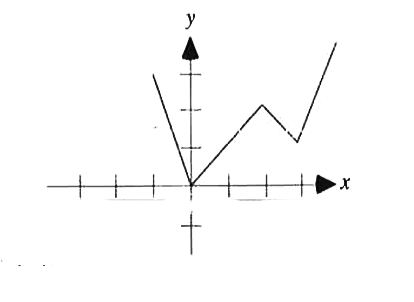
The graph of y=f(x) is shown to the right. If f(−1)=v, then which one of the following could be the value of f(v) ?
View SolutionWhich of the following could be the graph of y=3−2x ?
View SolutionWhich of the following could be the graph of 2x+3y+12=0 ?
View SolutionWhich of the following could be the graph of 2x+3y+12=0 ?
View Solution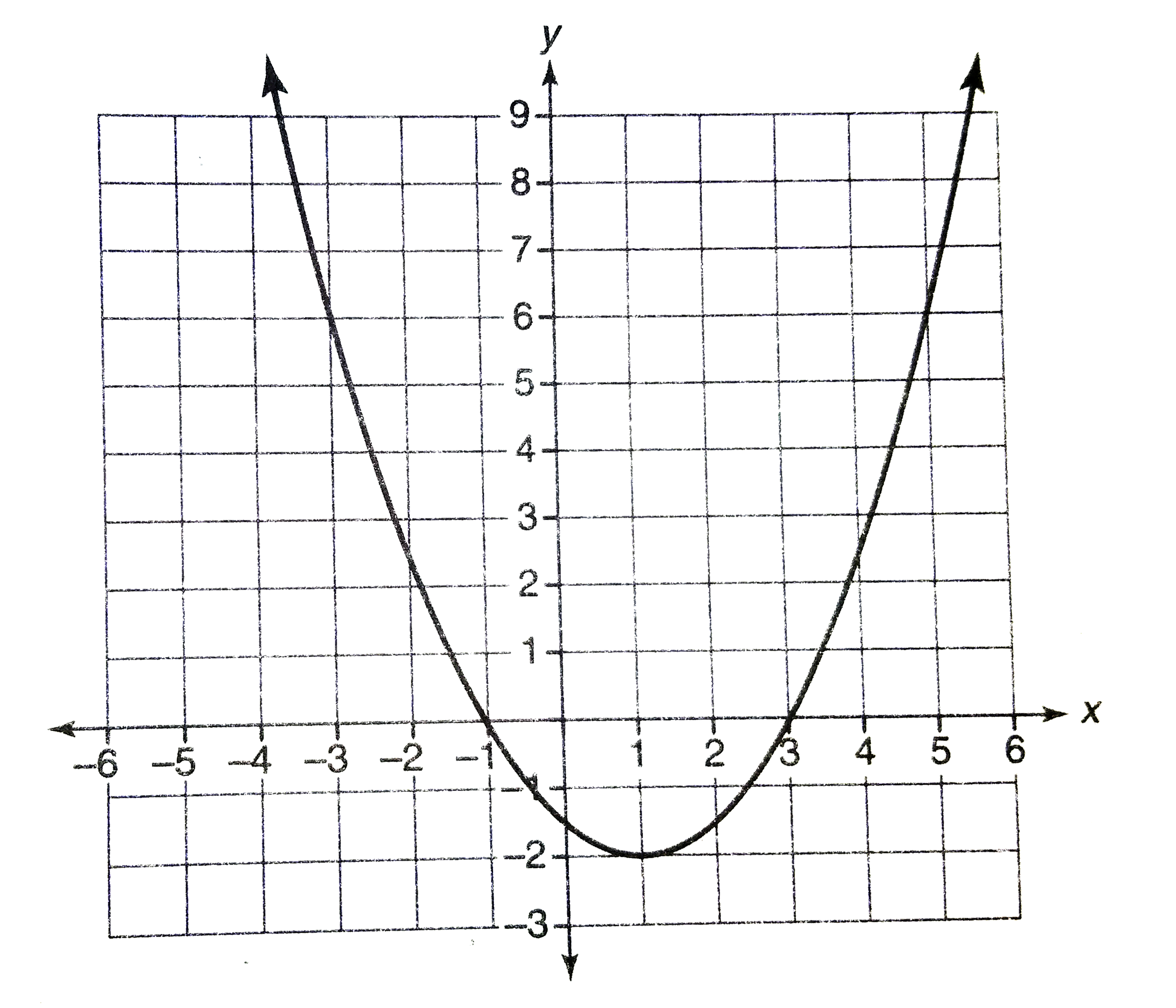
The figure above shows the graph of the quadratic function f with a minimum point at (1,−2). If f(5)=f(c), then which of the following could be the values of c?
View Solution
