A function @ is defined on positive integers as @(x)=(x+1)(x−1),and@(a)=3, then a =
−2
−1
0
2
The correct Answer is:A, D
To solve the problem step by step, we start with the function definition and the given condition.
Step 1: Understand the function definition
The function "@" is defined as:
@(x)=(x+1)(x−1)
This can also be expressed using the difference of squares:
@(x)=x2−1
Step 2: Set up the equation based on the given condition
We are given that:
@(a)=3
Substituting the function definition into this equation gives:
a2−1=3
Step 3: Solve for a2
To isolate a2, we add 1 to both sides of the equation:
a2−1+1=3+1
This simplifies to:
a2=4
Step 4: Take the square root of both sides
Taking the square root of both sides gives us:
a=±2
This means a can be either 2 or -2.
Step 5: Determine the valid solution
Since the function is defined on positive integers, we only consider the positive solution:
a=2
Conclusion
Thus, the value of a is:
2
---
The function "@" is defined as:
@(x)=(x+1)(x−1)
This can also be expressed using the difference of squares:
@(x)=x2−1
We are given that:
@(a)=3
Substituting the function definition into this equation gives:
a2−1=3
To isolate a2, we add 1 to both sides of the equation:
a2−1+1=3+1
This simplifies to:
a2=4
Taking the square root of both sides gives us:
a=±2
This means a can be either 2 or -2.
Since the function is defined on positive integers, we only consider the positive solution:
a=2
Thus, the value of a is:
2
Similar Questions
Knowledge Check
A function @ is defined on positive integers as @(a)=@(a−1)+1. If the value of @(1) is 1, then @(3) equals which one of the following?
A0B1C2D3If function f defined on th set of integers f(x) = ⎧⎪⎨⎪⎩1+x1≤x<22x−12≤x<43x−104≤x<6
AzBI+C{1,2,3,4,5}D(3,6,9,12,18}f (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?A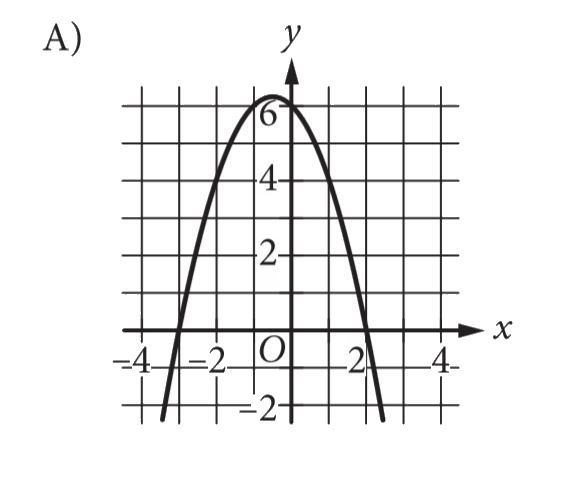 B
B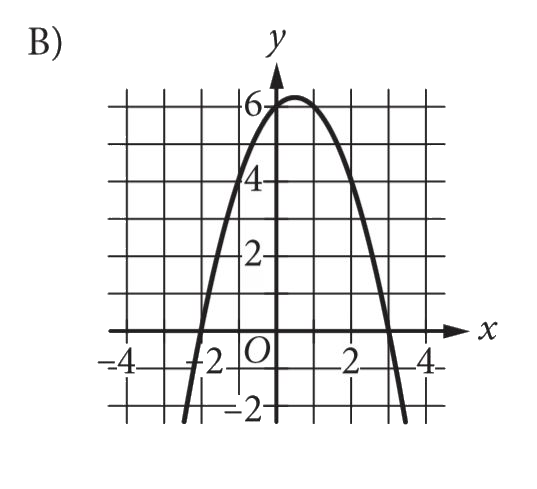 C
C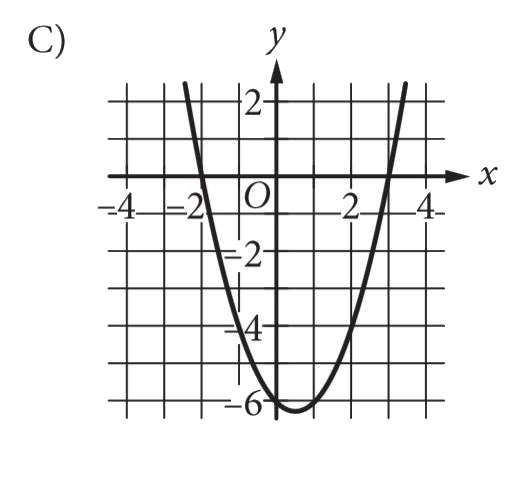 D
D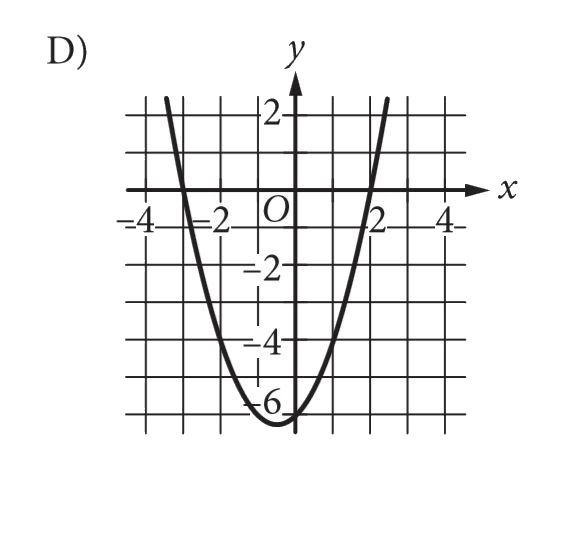
If x and y are positive integers such that tan−1x+cot−1y=tan−13, then:
View SolutionThe function f:R→R is defined by f(x)=(x−1)(x−2)(x−3) is
View SolutionFind the number of positive integers x satisfying the equation 1x+1x+1+1x+2=1312.
View SolutionThe function f is defined by f(x)=13(x3+x2−11x−3) .
If p1,p2 and p3 are the zeros of f(x). Find the product p1p2p3 to the nearest integer.
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1) then f−1(x) is
View Solution