Which of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
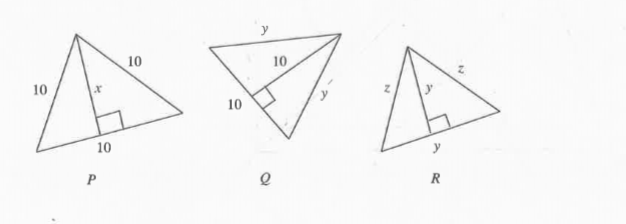
I = II = III
I lt II lt III
I gt II lt III
III lt I lt II
The correct Answer is:B
Similar Questions
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Which of the following statements is/are correct?
1. The area of triangle ABC is equal to four times the area of triangle BED.
2. The area of triangle ADC is twice the area of triangle BED.
Select the correct answer using the code given below.
View SolutionA square, a circle and equilateral triangle have same perimeter. Consider the following statements. I. The area of square is greater than the area of the triangle. II. The area of circle is less than the area of triangle. Which of the statement is/are correct?
View Solution
Knowledge Check
The area of rectangle is twice the area of a triangle. The p"rimeter of the rectangle is 58 cm. What is the area of the triangle ?
A106cm2B108cm2C104cm2DCannot be determinedWhat is the height of the right angle triangle ? I. It is a right-angled triangle. II. The area of the triangle is 5 times its base.
Aif the data in statement I alone are sufficient to answer the questin, while the data in statement II alone are not sufficient to answer the question.Bif the data in statement II alon are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question.Cif the data either in statement I alone or in statement II alone in sufficient to answer the question.Dif the data in both the statements I and II together are necessary to answer the question.
Equilateral triangles I, II, Ill and IV are such that the altitude of triangle I is the side of triangle II, the altitude of triangle II is the side of triangle Ⅲ and the altitude of the triangle is the side of triangle IV. If the area of triangle I is 2 cm2, then the area (incm2) of triangle IV is:
View SolutionLet ABCD be a parallelogram. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Consider the following statements :
1. Area of triangle APS < Area of triangle DSR if BD<AC.
2. Area of triangle ABC = 4 (Area of triangle BPQ).
Select the correct answer using the code given below :
View SolutionConsider the following statements :
1. Let D be a point on the side BC of a triangle ABC: If area of triangle ABD = area of triangle ACD, then for all points O on AD, area of triangle ABO = area of triangle ACO.
2. If G is the point of concurrence of the medians of a triangle ABC, then area of triangle ABG = area of triangle BCO = area of triangle ACG.
Which of the above statements is/are correct?
View SolutionA square, a circle and an equilateral triangle have same perimeter. Consider the following statements :
1. The area of square is greater than the area of the triangle.
2. The area of circle is less than the area of triangle .
Which of the statements is/are correct ?
View SolutionIn a triangle PQR , let ∠PQR=30o and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE? ∠QPR=45o (b) The area of the triangle PQR is 25√3 and ∠QRP=120o (c) The radius of the incircle of the triangle PQR is 10√3−15 (d) The area of the circumcircle of the triangle PQR is 100 π
View SolutionABCD is rectangle. P and Q are points on ABandBC respectively such that the area of triangle APD=5, area of triangle PBQ=4 and area of triangle QCD=3, all areas in square units. Then the areaof the triangle DPQ in square units is
View Solution
