Column AThe perimeter of rectangle ABCD is 5/2 times as long as the side ABColumn BLength of side ABLength of side BC
If column A is larger
If column B is larger
If the columns are equal
If there is not enough information to decide
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the sides of rectangle ABCD based on the given information about its perimeter.
1. Define the sides of the rectangle:
Let the length of side AB be denoted as X and the length of side BC be denoted as Y.
2. Write the formula for the perimeter of a rectangle:
The perimeter P of a rectangle is given by the formula:
P=2×(L+B)=2×(X+Y)
3. Set up the equation based on the given information:
According to the problem, the perimeter of rectangle ABCD is 52 times the length of side AB. Therefore, we can write:
2×(X+Y)=52×X
4. Simplify the equation:
We can simplify the equation:
2X+2Y=52X
To eliminate the fraction, multiply the entire equation by 2:
4X+4Y=5X
5. Rearranging the equation:
Rearranging gives us:
4Y=5X−4X
4Y=X
6. Express Y in terms of X:
Dividing both sides by 4, we find:
Y=14X
7. Compare the lengths of sides AB and BC:
Since AB=X and BC=Y, we can express the relationship:
AB=4×BC
This shows that the length of side AB is greater than the length of side BC.
Conclusion:
From the analysis, we conclude that the length of side AB is greater than the length of side BC. Therefore, the answer to the comparison in the columns is that Column A (Length of side AB) is greater than Column B (Length of side BC).
Let the length of side AB be denoted as X and the length of side BC be denoted as Y.
The perimeter P of a rectangle is given by the formula:
P=2×(L+B)=2×(X+Y)
According to the problem, the perimeter of rectangle ABCD is 52 times the length of side AB. Therefore, we can write:
2×(X+Y)=52×X
We can simplify the equation:
2X+2Y=52X
To eliminate the fraction, multiply the entire equation by 2:
4X+4Y=5X
Rearranging gives us:
4Y=5X−4X
4Y=X
Dividing both sides by 4, we find:
Y=14X
Since AB=X and BC=Y, we can express the relationship:
AB=4×BC
This shows that the length of side AB is greater than the length of side BC.
From the analysis, we conclude that the length of side AB is greater than the length of side BC. Therefore, the answer to the comparison in the columns is that Column A (Length of side AB) is greater than Column B (Length of side BC).
Similar Questions
Knowledge Check
- Question 1 - Select One
The perimeter of rectangle ABCD is 96 cm. The ratio of the side lengths AB : BC is 3:5. What is the length, in centimeters of ¯¯¯¯¯¯AB?
A6B18C30D36 - Question 2 - Select One
In the figure, if AB = 10, what is the length of the side CD ?
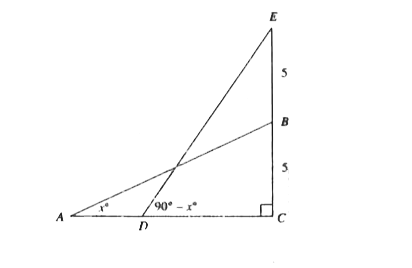 A5B5√3C10√3D10
A5B5√3C10√3D10 - Question 3 - Select One
In triangle ABC, AB = 5 and AC = 3. which one of the following is the measure of the length of side BC?
ABC<7BBC=7CBC>7DIt cannot be determined from the information given
In rectangle ABCD, slope of AB=56. State the slope of
BC .View SolutionFind the perimeters of :
A square having each side of length 4.5 cm.View SolutionIf the perimeter of an equilateral triangle is 40.5 cm, what is the length of its side?
View SolutionFind the perimeters of :
A triangle ABC having sides of lengths , AB=7 cm , BC =5 cm , AC = 8.5 cmView SolutionColumn A Column BMeasure of the largest angle(in degree) of a triangle with sides of length 5,6 and 760
View Solution

