If (−3,−5) is the midpoint of the part of the line between the x and y axes, then what is the slope of the line?
−5/3
−3/5
3/5
5/3
The correct Answer is:A
To find the slope of the line given that the point (−3,−5) is the midpoint of the segment between the x-axis and y-axis, we can follow these steps:
Step 1: Identify the points on the axes
Let the point where the line intersects the x-axis be A(a,0) and the point where it intersects the y-axis be B(0,b).
Step 2: Use the midpoint formula
The midpoint M of the segment AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(a+02,0+b2)=(a2,b2)
Given that the midpoint M is (−3,−5), we can set up the equations:
a2=−3andb2=−5
Step 3: Solve for a and b
From the first equation:
a=−3×2=−6
From the second equation:
b=−5×2=−10
Thus, the coordinates of points A and B are A(−6,0) and B(0,−10).
Step 4: Calculate the slope of the line
The slope m of the line passing through points A and B is given by:
m=y2−y1x2−x1=−10−00−(−6)=−106=−53
Final Answer
The slope of the line is:
−53
---
Let the point where the line intersects the x-axis be A(a,0) and the point where it intersects the y-axis be B(0,b).
The midpoint M of the segment AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(a+02,0+b2)=(a2,b2)
Given that the midpoint M is (−3,−5), we can set up the equations:
a2=−3andb2=−5
From the first equation:
a=−3×2=−6
From the second equation:
b=−5×2=−10
Thus, the coordinates of points A and B are A(−6,0) and B(0,−10).
The slope m of the line passing through points A and B is given by:
m=y2−y1x2−x1=−10−00−(−6)=−106=−53
The slope of the line is:
−53
Similar Questions
A line makes a postitive X - intercept and a negative Y - intercept and has a slope equal of 43. If the coordinates of the points where the line intersects the X and Y axes are integers, what is the angle formed by the line with the X and Y axes ?
View SolutionThe slope of a line is double of the slope of another line. If tangents of the angle between the is find the slopes of the other line.
View Solution
Knowledge Check
What is the slope of the line 2(x+2y)=0
A12B−2C−12D0A line passes through P(1,2) such that the portion of the line intercepted between the axes is bisected at P. The equation of the line is
Ax+2y−5=0Bx−y+1=0Cx+y−3=0D2x+y−4=0In the standard (x,y) coordinate plane, what is the slope of the line 3x+8y=5?
A−3B−38C35D3
The slope of a line is double of the slope of another line. If tangent of the angle between them is 13, find the slopes of the lines.
View SolutionP (a, b) is the midpoint of a line segment between axes. Show that equation of the line is xa+yb=2.
View Solution(i) Find the equation of a line, in which the mid- point of the line segment between the axes is (−3,2).
(ii) Find the area of triangle formed by the line 4x+3y=24 and the co-ordinate axes.
View SolutionPoints (2,-2) and ((3,10) lie on the same line in the standed (x,y) coordinate plane . What is the slope of this line ?
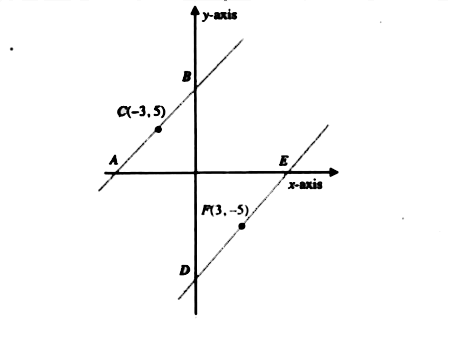
View SolutionColumn AIn the rectangular coordinate system shown, points A and E lie on the x-axis, and points B and D lie on the y-axis. Point C is the midpoint of the line AB and point F is the midpoint of the line DEColumn BThe slope of the line ABThe slope of the line DE
View Solution
