Four pool balls - A, B, C, D - are randomly arranged in a striaght line. What is the probability that the order will actually be A, B, C, D ?
1/4
1.4C4
1.4P4
1/3!
The correct Answer is:C
Step by step video, text & image solution for Four pool balls - A, B, C, D - are randomly arranged in a striaght line. What is the probability that the order will actually be A, B, C, D ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
On her vacations Veena visits four cities A, B, C and D in a random order. What is the probability that she visits: A before B?
View SolutionOn her vacations Veena visits four cities (A,B,CandD)in a random order. What is the probability that she visits(i) A before B?(ii) A before B and B before C?(iii) A first and B last?(iv) A either first or second?(v) A just be
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, AOB is a straight line. What is the average of the four number, a, b , c, d ?
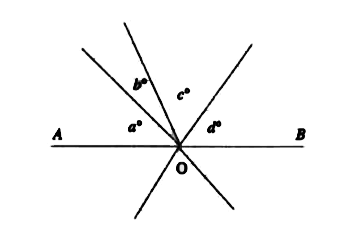 A45B360/7C60D90
A45B360/7C60D90 - Question 2 - Select One
Four men A,B,C and D, line up in a row. What is the probability that man A is at either end of the row?
A12B13C14D16
In a really race there are give teams, A, B, C, D and E i. What is the probability that A, B, and C finish first, second and third respectively. ii. What is the probability that A, B and C are first three to finish (in any order).
View SolutionIn a relay race there are five teams A. B, C. D and E.(a) What is the probability that A. B and C finish first, second and third, respectively.(b) What is the probability that A. B and C are first three to finish (in any order) (Assume that all finishing orders are equally likely).
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionFour candidates A, B, C, D have applied for the assignment ot coach a school cricket team. If A is twice as likely to be selected as B, and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probability that (i) C will be selected ? (ii) A will not be selected?
View SolutionFour candidates A, B, C, D have applied for the assignment ot coach a school cricket team. If A is twice as likely to be selected as B, and B and C are given about the same chance of being selected, while C is twice as likely to be selected as D, what are the probability that (i) C will be selected ? (ii) A will not be selected?
View Solution

