Fritz is taking an examination that consists of two parts , A and B , with the following instructions:
Part A contains three questions, and a student must answer tow .
Part B contains four questions, and a student must answer two.
Part A must be completed before starting part B.
How many ways can the test be completed?
12
15
36
72
The correct Answer is:D
To solve the problem step by step, we will calculate the number of ways Fritz can complete the examination by choosing questions from both parts A and B.
Step 1: Calculate the number of ways to choose questions from Part A
Part A contains 3 questions, and Fritz must answer 2 of them. The number of ways to choose 2 questions from 3 can be calculated using the combination formula:
Number of ways to choose 2 from 3=(32)=3!2!(3−2)!=3!2!⋅1!=3×2×1(2×1)⋅(1)=3
Step 2: Calculate the number of ways to choose questions from Part B
Part B contains 4 questions, and Fritz must answer 2 of them. The number of ways to choose 2 questions from 4 can also be calculated using the combination formula:
Number of ways to choose 2 from 4=(42)=4!2!(4−2)!=4!2!⋅2!=4×3×2×1(2×1)⋅(2×1)=244=6
Step 3: Calculate the total number of ways to complete the test
Since Part A must be completed before Part B, we multiply the number of ways to choose questions from both parts:
Total ways=Ways from Part A×Ways from Part B=3×6=18
Final Answer
Thus, the total number of ways Fritz can complete the test is 18.
Part A contains 3 questions, and Fritz must answer 2 of them. The number of ways to choose 2 questions from 3 can be calculated using the combination formula:
Part B contains 4 questions, and Fritz must answer 2 of them. The number of ways to choose 2 questions from 4 can also be calculated using the combination formula:
Since Part A must be completed before Part B, we multiply the number of ways to choose questions from both parts:
Thus, the total number of ways Fritz can complete the test is 18.
Similar Questions
A question paper has two parts, Part A and party B each containing 10 questions. If a student has to chose 8 from Part A and 5 from Part B, in how many ways can he choose the questions?
View SolutionA student has to answer 10 questions, choosing at least 4 from each of part A and B. If there are 6 questions in part A and 7 in part B. In how many ways can the student choose 10 questions?
View SolutionIn an examination, a question pater consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a students select the questions ?
View SolutionIn an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
View SolutionA mathematics paper consists of 10 questions divided into two parts I and II each part containing 5 questions. A student is required to attempt 6 questions in al, taking at least 2 questions from each part. In how many ways can student select the questions?
View SolutionA test contains 10 true/false questions. A correct answer is awarded 2 marks, a wrong answer -1 and a question not answered is awarded 0. A student attempts 7 questions and gets 8 marks. How many questions did the student answer correctly?
View SolutionStudy this structure of a root hair and answer the following:
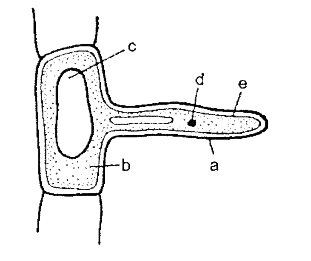
Label parts a, b, c, d and e.View SolutionA question paper on mathematics consists of 12 questions divided in to 3 pars A, B and C, each containing 4 questions. In how many ways can an examinee answer questions selecting at least one from each part.
View SolutionA question paper on mathematics consists of 12 questions divided into 3 parts A, B and C, each containing 4 questions. In how many ways can an examinee answer 5 questions selecting at least one from each part.
View SolutionIn how many ways can a ten question multiple choice examination be answered if there are four choices a, b, c and d to each question? If no two consecutive questions are answered the same way, how many ways are there?
View Solution

