If f(2010)=π/2,f(2x)=f(x)∀x∈R and f(x) is continuous for x∈R, then the value of limx→0cos(f(x))−3√cos(f(x))sin2x is Limx→π/2[x−π2cosx] is
A
1/4
B
1
C
0
D
None of these
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE -2( LEVEL-I)
16 Videos
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-2(LEVEL-2)
5 Videos
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-4
17 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - MOTIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise -4 Level -II
7 Videos
- MATRICES BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)
28 Videos
Similar Questions
Knowledge Check
The graph of the function f(x)=Limt→0(2xπcot−1xt2), is
A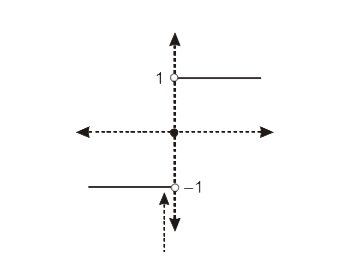 B
B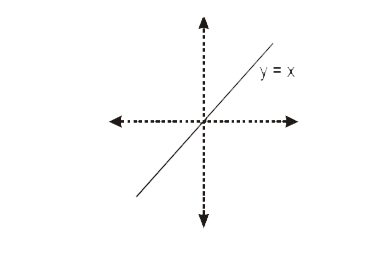 C
C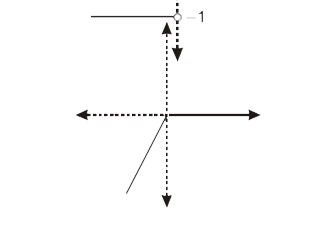 D
D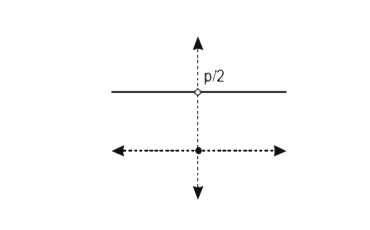
f'(x)=∣∣ ∣ ∣∣cosxx12sinxx22xtanxx1∣∣ ∣ ∣∣ . The value of limx→0f(x)x is equal to
A1B−1C0DNone of theseIf l=Limx→0x(1+acosx)−bsinxx3=Limx→01+acosxx2−limx→0bsinxx3 , where l∈R, then
A(a,b)=(−1,0)Ba & b are nay real numbersCl = 0Dl=12
If f(x) is the integral of 2sinx−sin2xx3,where x≠0,then findlimx→0f'(x).
View Solutionf(x) is the function such that Limx→0f(x)x=1.
If Limx→0x(1+acosx)−bsinx(f(x))3=1 , then find the value of a and b.
View Solutionlimx→0cos(π2cosx)sin(sinx2)
View Solutionlimx→0(sin(πcos3x)x2)=
View SolutionThe value of limx→0|x||cosx| is {[.]=g.i.f}
View Solution
