Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.

2 and 64

64 and 3

64 and 4

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video & text solution for Find two numbers whose arithmetic mean is 34 and the geometric mean is 16. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS SEQUENCE & SERIES

Topper's Solved these Questions

BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -2 (Level -II) Multiple Correct /JEE Advanced
9videos
SEQUENCE & SERIES
BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -3 Subjective /JEE Advanced
35videos
SEQUENCE & SERIES
BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -1 Objective Problems /JEE Main Section -A : AP
24videos
SEQUENCE & SERIES
BOOK - MOTIONCHAPTER - QUADRATIC EQUATIONEXERCISE - EXERCISE 4 (PREVIOUS YEAR| JEE MAIN)
25videos
QUADRATIC EQUATION
BOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 4( LEVEL II)
10videos
SOLUTION OF TRIANGLE

Knowledge Check

Question 1 - Select One
The harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If $2 A + G^{2} = 27, a + b = α$ and $| a - b | = β$ , then the value of $\frac{α}{β}$ is equal to
A1
B3
C $\frac{5}{2}$
D5
Question 2 - Select One
What will be quadratic equation in x when the roots have arithmetic mean A and the geometric mean G?
A $x^{2} + 2 A x + G^{2} = 0$
B $x^{2} + G^{2} x + A = 0$
C $x^{2} - 2 A x + G^{2} = 0$
D $x^{2} + G x + A = 0$
Question 3 - Select One
Find the arithmetic mean of:

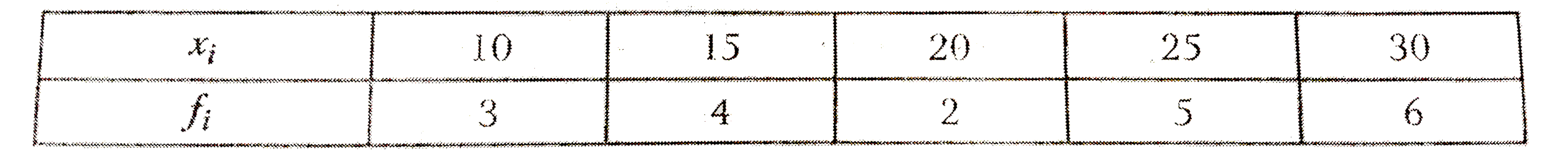A21
B21.4
C22.75
D21.75

MOTION-SEQUENCE & SERIES -Exercise -2 (Level -I) Objective Problems /JEE Main AP

Home
Ask Doubt
Profile

Find two numbers whose arithmetic mean is 34 and the geometric mean is 16.

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

The harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If 2A+G2=27,a+b=α and |a−b|=β, then the value of αβ is equal to

What will be quadratic equation in x when the roots have arithmetic mean A and the geometric mean G?

Find the arithmetic mean of:

MOTION-SEQUENCE & SERIES -Exercise -2 (Level -I) Objective Problems /JEE Main AP

The harmonic mean of two positive numbers a and b is 4, their arithmetic mean is A and the geometric mean is G. If $2 A + G^{2} = 27, a + b = α$ and $| a - b | = β$ , then the value of $\frac{α}{β}$ is equal to