Circles are inscribed in the acute angle α so that every neighbouring circles touch each other. If the radius of the first circle is R then find the sum of the radii of the first n circles in terms of R and α.
R(1−sin.α2)2sin.α2[(1+sin.α21−sin.α2)n−1]
Topper's Solved these Questions
- SEQUENCE & SERIES BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -3 Subjective /JEE Advanced (Comprehension )
3 Videos
- SEQUENCE & SERIES BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -4 Level -I Previous Year /JEE Main
19 Videos
- SEQUENCE & SERIES BOOK - MOTIONCHAPTER - SEQUENCE & SERIES EXERCISE - Exercise -2 (Level -II) Multiple Correct /JEE Advanced
9 Videos
- QUADRATIC EQUATIONBOOK - MOTIONCHAPTER - QUADRATIC EQUATIONEXERCISE - EXERCISE 4 (PREVIOUS YEAR| JEE MAIN)
25 Videos
- SOLUTION OF TRIANGLEBOOK - MOTIONCHAPTER - SOLUTION OF TRIANGLEEXERCISE - EXERCISE - 4( LEVEL II)
10 Videos
Similar Questions
(a,c)and(b,c) are the centres of two circles whose radical axis is the y-axis. If the radius of the first circle is r then the diameter of the other circle is
View SolutionIf a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View Solution
Knowledge Check
Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2The areas of a square and a circle are equal. The radius of the circle is r and the side of the square is S.Find the circumference of the circle in terms of S.
ASB2SC3SD4SIf the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
AR1+R2=RBR21+R22=R2CR1+R2<RDR21+R22<R2
If a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View SolutionFind the area of right triangle if it is known that the radius of the circle inscribed in the triangle is r and that of the circumscribed circle is R.
View SolutionThe radius of a circle is greater than the radius of other circle by 3 m. The sum of their areas is 89πm2 . Find the radius of each circle.
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
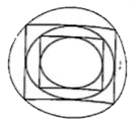
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
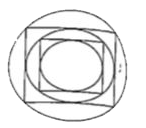
What is the sum of areas of all the squares shown in the figure ?
View Solution
