The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

mgk
2mgk
mg2k
mg4k
The correct Answer is:B
Step by step video, text & image solution for The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 3 Section-A25videos
WORK, POWER & ENERGY
- BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 3 Section-B22videos
WORK, POWER & ENERGY
- BOOK - MOTIONCHAPTER - WORK, POWER & ENERGY EXERCISE - Exercise - 142videos
WORK, POWER & ENERGY
- BOOK - MOTIONCHAPTER - WAVESEXERCISE - EXERCISE -4 (Level -II) (previous year JEE Advanced)10videos
WAVES
Similar Questions
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionTwo blocks of mass m and 2m are connected to a spring and wrapped around a smooth pulley as shown in the figure. Blocks are released together with spring in natural length. Calculate the maximum elongation (in meter) of the spring. Given mgK=3 meter.
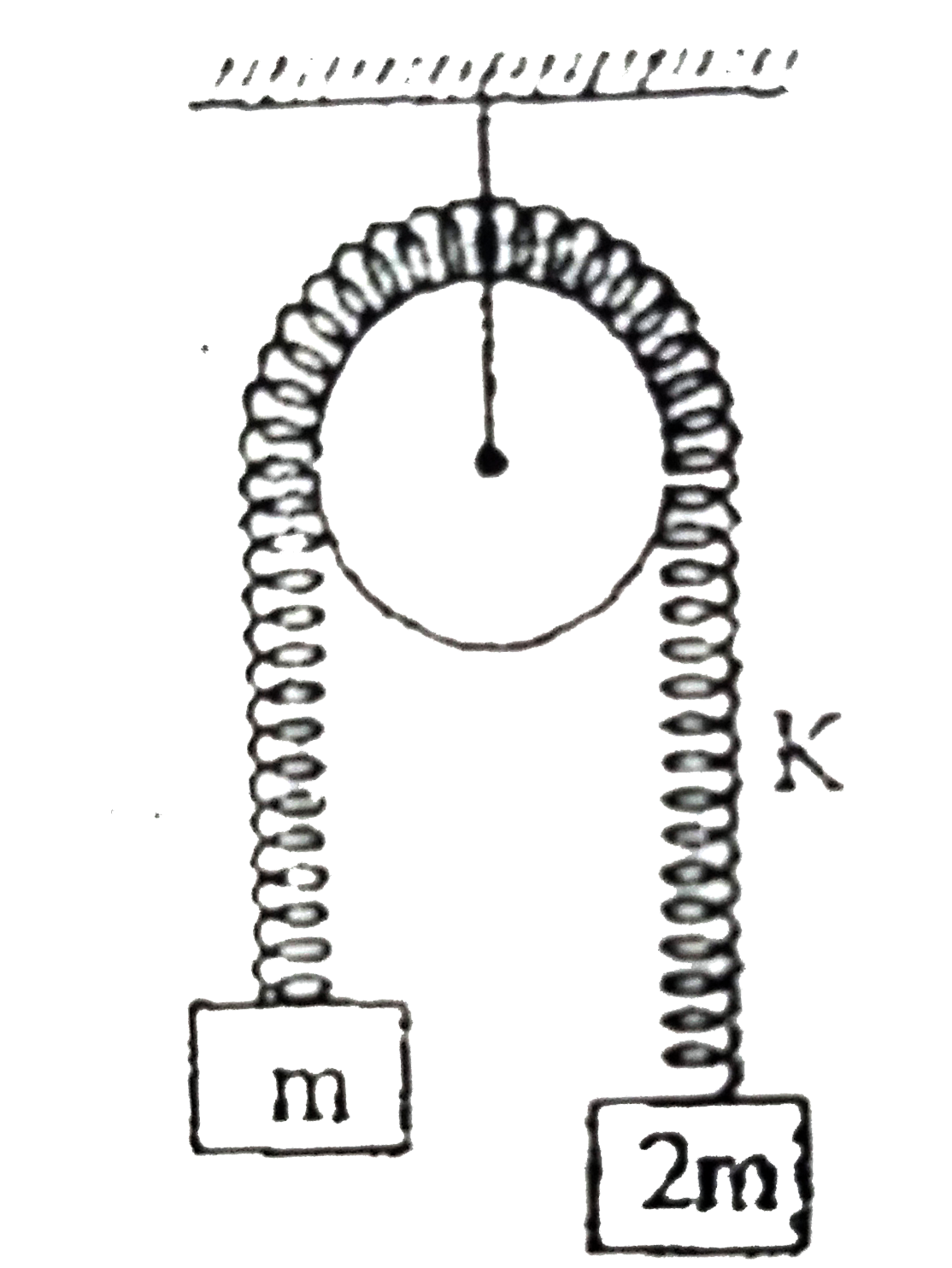 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
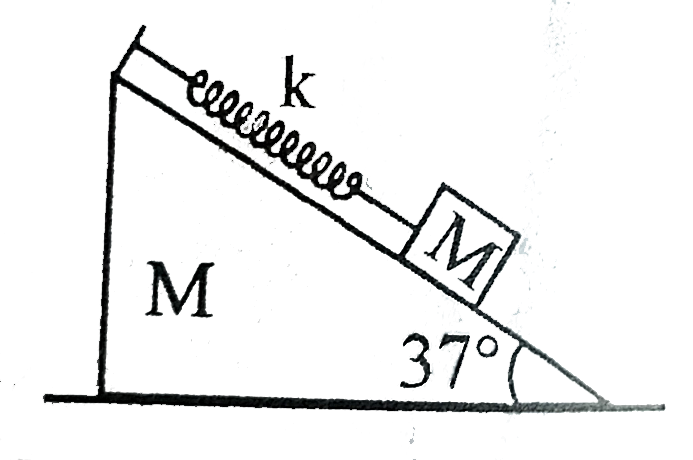 A3Mg5kB6Mg5kC4Mg5kD8Mg5k
A3Mg5kB6Mg5kC4Mg5kD8Mg5k - Question 2 - Select One
A system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 . A2mgsinθKBmgsinθKC4mgsinθKDmgsinθ2K
. A2mgsinθKBmgsinθKC4mgsinθKDmgsinθ2K - Question 3 - Select One
In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
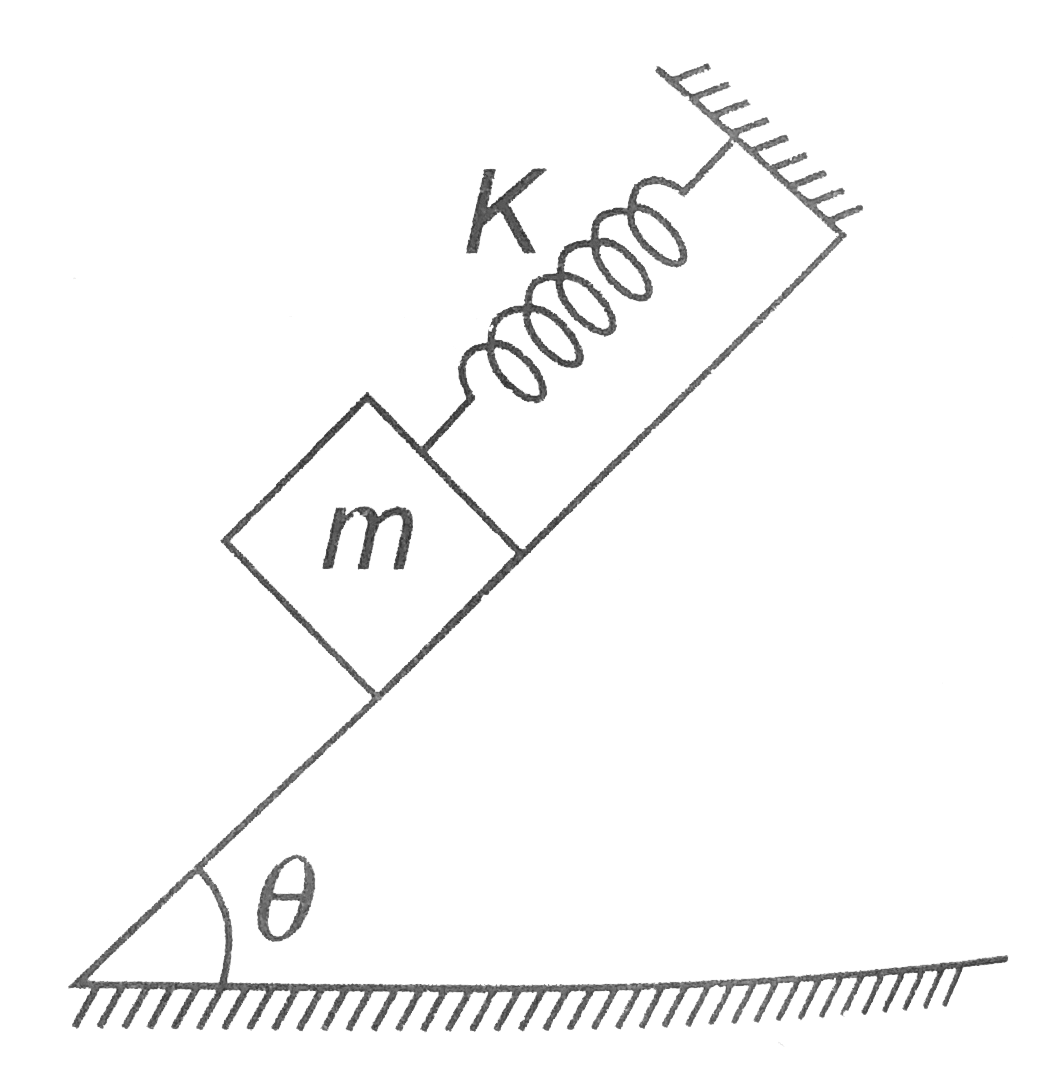 A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
In figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
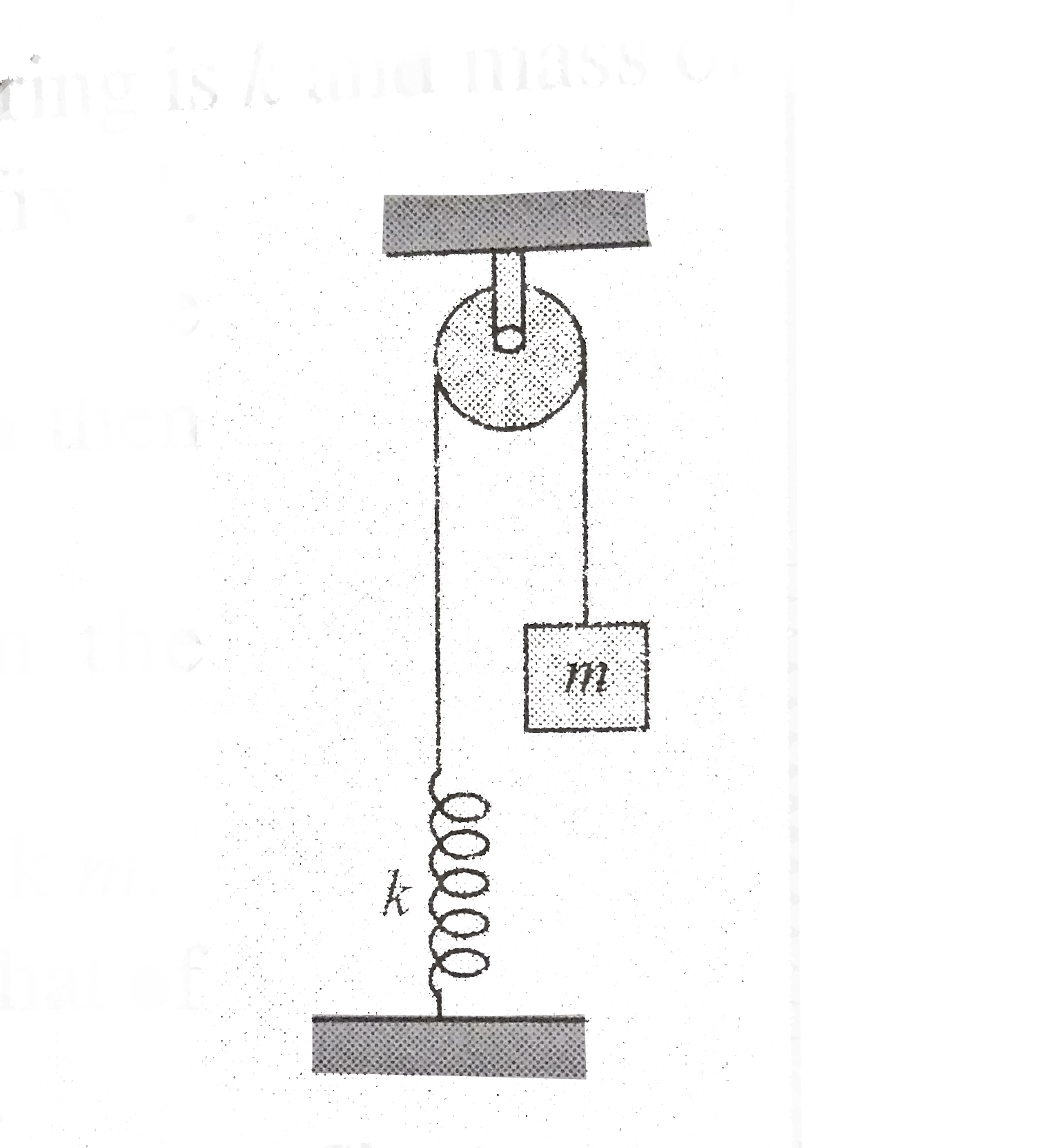 View Solution
View SolutionA block of 2 kg is suspended from the ceiling trhough a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is dded to the block, what would be the further eleongation?
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
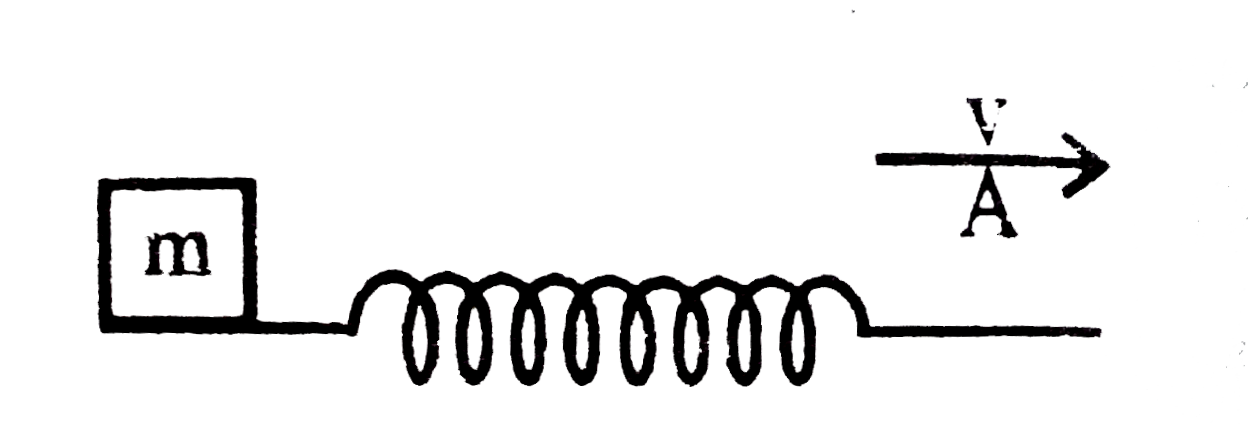 View Solution
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
 View Solution
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solution

