A ray of light travels through a transparent slab with a speed of 2×1010cms−1. This implies that therefractive index of the slab material is
1.5
0.667
2.0
6.0
The correct Answer is:A
To find the refractive index of the slab material based on the speed of light traveling through it, we can follow these steps:
Step 1: Identify the speed of light in vacuum
The speed of light in vacuum (C) is approximately:
C=3×108 m/s
Step 2: Identify the speed of light in the slab
The speed of light in the slab (V) is given as:
V=2×1010 cm/s
To convert this to meters per second, we use the conversion factor 1 cm=0.01 m:
V=2×1010 cm/s=2×1010×0.01 m/s=2×108 m/s
Step 3: Use the formula for refractive index
The refractive index (n) is defined as the ratio of the speed of light in vacuum to the speed of light in the medium:
n=CV
Step 4: Substitute the values into the formula
Substituting the known values:
n=3×108 m/s2×108 m/s
Step 5: Simplify the expression
Now, simplify the fraction:
n=32=1.5
Conclusion
Thus, the refractive index of the slab material is:
n=1.5
The speed of light in vacuum (C) is approximately:
C=3×108 m/s
The speed of light in the slab (V) is given as:
V=2×1010 cm/s
To convert this to meters per second, we use the conversion factor 1 cm=0.01 m:
V=2×1010 cm/s=2×1010×0.01 m/s=2×108 m/s
The refractive index (n) is defined as the ratio of the speed of light in vacuum to the speed of light in the medium:
n=CV
Substituting the known values:
n=3×108 m/s2×108 m/s
Now, simplify the fraction:
n=32=1.5
Thus, the refractive index of the slab material is:
n=1.5
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-239videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-365videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Questions For Practice29videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RADIOACTIVITY & NUCLEAR PHYSICSEXERCISE - Exercise-381videos
RADIOACTIVITY & NUCLEAR PHYSICS
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )24videos
ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Light travels through water with a speed of 2.25×108m/s. What is the refractive index of water ? Given speed of light in vacuum =3×108m/s.
A1.41B1.47C1.33D1.5 - Question 2 - Select One
The refractive index of glass is 1.9. If light travels through a glass slab of thickness d in time t and takes the same time to travel through a transparent beaker filled with water upto a level of 1.5 d, then the refractive index of water is
A1.27B1.33C1.20D1.50 - Question 3 - Select One
A ray of light in air is incident on a glass slab at an angle of incidence of 60∘. When it travels through glass, it is deviated through 15∘. What is the refractive index of the material of the glass slab ?
A1.275B1.225C1.8D1.5
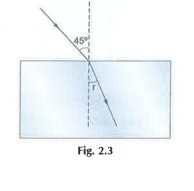
A ray of light travelling in air falls on the surface of a transparent slab. The ray makes an angle of 45∘ with the normal to the surface. Find the angle made by the refracted ray with the normal within the slab. Refractive index of the material of the slab =√2.
 View Solution
View SolutionAn object viewed directly through a rectangular slan 12 cm thick appears to be raised by 4 cm. The refractive index of the material of slab is ________.
View SolutionThe lateral shift for a ray of light incident at 60∘ on one face of a rectangular slab of thickness 1 m is 0.577 m. What is the refractive index of the slab.
View SolutionA ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.
 View Solution
View SolutionA ray of light travelling in air is incident on a composite transparent slab at an angle of incidence i=45°. The composite slab consist of 100 parallel faced slices of equal thickness. The refractive index of the nth slice (counting from the one on which light is incident) is given by μn=1.0+0.01n. The medium on the other side of the slab has refractive index of √2 . Calculate the angular deviation suffered by the ray as it comes out of the slab.
View Solution

