Focal length of convex lens is f. If this lens is cut along parallel to its length in two equal parts then focal length of its half part will be:
f/2
f
3f2
2f
The correct Answer is:A
To solve the problem of finding the focal length of a half part of a convex lens when the original lens has a focal length of f, we can follow these steps:
1. Understanding the Lens Maker's Formula:
The lens maker's formula is given by:
1f=(μ2μ1−1)(1R1−1R2)
where f is the focal length of the lens, μ1 is the refractive index of the medium from which light is coming (air, μ1=1), μ2 is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the lens surfaces.
2. Applying the Formula to the Original Lens:
For the original convex lens with focal length f:
1f=(μ−1)(1R1−1R2)
3. Cutting the Lens in Half:
When the lens is cut in half parallel to its length, one part will have a curved surface and the other will have a plane surface. Let’s denote the focal length of the half lens as f′.
4. Analyzing the Half Lens:
For the half lens:
- The first surface remains curved with radius R.
- The second surface becomes a plane surface, which can be treated as having an infinite radius of curvature (R2=∞).
5. Using the Lens Maker's Formula for the Half Lens:
The lens maker's formula for the half lens becomes:
1f′=(μ−1)(1R−1∞)=(μ−1)1R
6. Relating the Focal Lengths:
From the original lens, we have:
1f=(μ−1)(1R1−1R2)
If we assume R1=R and R2=−R for a symmetric lens, we can express:
1f=(μ−1)(1R+1R)=2(μ−1)1R
Thus, we can relate 1R to 1f:
1R=12f(μ−1)
7. Substituting Back:
Substituting 1R back into the equation for f′:
1f′=(μ−1)1R=(μ−1)⋅12f=(μ−1)2f
Thus, we can conclude:
f′=2f
Conclusion:
The focal length of the half part of the convex lens is 2f.
The lens maker's formula is given by:
1f=(μ2μ1−1)(1R1−1R2)
where f is the focal length of the lens, μ1 is the refractive index of the medium from which light is coming (air, μ1=1), μ2 is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the lens surfaces.
For the original convex lens with focal length f:
1f=(μ−1)(1R1−1R2)
When the lens is cut in half parallel to its length, one part will have a curved surface and the other will have a plane surface. Let’s denote the focal length of the half lens as f′.
For the half lens:
- The first surface remains curved with radius R.
- The second surface becomes a plane surface, which can be treated as having an infinite radius of curvature (R2=∞).
The lens maker's formula for the half lens becomes:
1f′=(μ−1)(1R−1∞)=(μ−1)1R
From the original lens, we have:
1f=(μ−1)(1R1−1R2)
If we assume R1=R and R2=−R for a symmetric lens, we can express:
1f=(μ−1)(1R+1R)=2(μ−1)1R
Thus, we can relate 1R to 1f:
1R=12f(μ−1)
Substituting 1R back into the equation for f′:
1f′=(μ−1)1R=(μ−1)⋅12f=(μ−1)2f
Thus, we can conclude:
f′=2f
The focal length of the half part of the convex lens is 2f.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-239videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-365videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Questions For Practice29videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - RADIOACTIVITY & NUCLEAR PHYSICSEXERCISE - Exercise-381videos
RADIOACTIVITY & NUCLEAR PHYSICS
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )24videos
ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Focal length of a convex lens is 25 cm. Its power is
A+4 DB−4 DC−0.4 DD+0.4 D - Question 2 - Select One
Focal length of a convex lens is maximum for
Ablue lightByellow lightCgreen lightDred light - Question 3 - Select One
Focal length of a lens is 20 cm. Its power
A+5DB- 5DC+ 5 cmD0.20 m
Focal length of convex lens will miximum for
View SolutionThe focal length of a convex lens is 50 cm . Its power is
View SolutionFocal length of a convex lens will be maximum for
View SolutionFocal length of a convex lens will be maximum for
View Solution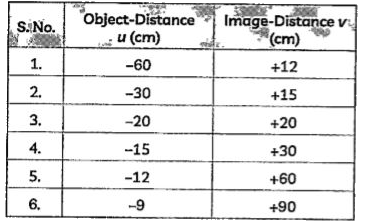
The focal length of the convex lens isView Solution

