The pressure at equilibrium over solid A is 50 atm and over solid D is 68 atm if both solid A and D are heated simultaneously .Find: relative number of moles of A ′and B in the vapour phase over a mixture of the solids A and B.
A(s)⇔B(g)x+y+C(g)x,Kp1=(25)2
D(s)⇔B(g)x+y+E(g)y,Kp2=(34)2
Kp1=(x+y)×x …(i)
Kp2=(x+y)×y …(ii)
total pressure =PB=PC+pE=x+y+x+y=2(x+y)
Also Kp1+kp2=(x+y)2
⇒x+y=√Kp1+Kp2
⇒x+y=√Kp1+Kp2
⇒ Total pressure =2(x+y)=2√Kp1+Kp2
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - SOLVED EXAMPLES
10 Videos
- CHEMICAL EQUILIBRIUMBOOK - MOTIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise - 1
45 Videos
- CHEMICAL BONDING BOOK - MOTIONCHAPTER - CHEMICAL BONDING EXERCISE - EXERCISE -4 LEVEL-II
40 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)
1 Video
Similar Questions
The pressure at equilibrium over solid A is 50 atm and over solid D is 68 atm if both solid A and D are heated simultaneously then find
mole fraction of C
View SolutionThe pressure at equilibrium over solid A is 50 atm and over solid D is 68 atm if both solid A and D are heated simultaneously .Find: relative number of moles of A ′and B in the vapour phase over a mixture of the solids A and B.
View Solution
Knowledge Check
Two solids X and Y dissociate into gaseous products at a certain temperature as follows:
i. X(s)⇔A(g)+C(g) and
ii. Y(s)⇔B(g)+C(g)
At a given temperature, pressure over excess solid 'X' is 40 mm of Hg and total pressure over solid 'Y(s)' is 60 mm of Hg.
Now, answer the following questions:
The ratio of moles of A and B in the vapour state over a mixture of solids X and Y, is:A2:3B2:5C4:9D1:1A mixture of two immiscible liquids A and B, having vapour pressure in pure state obeys the following relationship if χA and χB are mole fractions of A and B in vapour phase over the solution
AP'A=PMχ'ABPA'PB'=WA×MwBMwA×WBCIf PA'>PB'thenχ'A<χBDIf PA'>PB'thennA<nBA mixture of two miscible liquids A and B is distilled under equilibrium conditions at 1 atm pressure. The mole fraction of A in solution and vapour phase are 0.30 and 0.60 respectively. Assuming ideal behaviour of the solution and the vapour, calculate the ratio of the vapour pressure of pure A to that of pure B.
A4B3.5C2.5D1.85
Two solid compounds A and B dissociate into gaseous products at 20∘C as
(i) A(s)⇔A'(g)+H2S(g)
(ii) B(s)⇔B'(g)+H2S(g)
At 20∘C pressure over excess solid A is 50 mm and that over excess solid B is 68 mm. Find
(a) The dissociation constants of A and B
(b) Relative number of mole of A' and B' in the vapour phase over a mixture of the solids A and B .
View SolutionTwo solid compounds A and B dissociate into gaseous products at 20∘C as
a. A(s)⇔A'(s)+H2S(g)
b. B(s)⇔B'(g)+H2S(g)
At 20∘C pressure over excess solid A is 50 mm and that over excess solid B is 68 mm. Find:
a. The dissociation constant of A and B
b. Relative number of moles of A' and B' in the vapour phase over a mixture of the solids A and B.
c. Show that the total pressure of gas over the solid mixture would be 84.4 mm.
View SolutionTwo solid compounds AandB dissociate into gaseous products at 20∘C as
(i) A(S)hARrA'(g)+H2S(g)(ii)B(S)⇔B'(g)+H2S(g)
At 20∘C pressure over excess solid Ais50mm and that over excess solid Bis68mm find,
(a) The dissociation constant of AandB
(B) Relative no. of moles ofAandB' in the vapour phase over a mixture of solid AandB.
(c) Show that the total pressure of the gas over the solid mixture would be 84.4mm
View SolutionTwo solid X and Y dissociate into gaseous products at a certain temperature as followas:
X(s)⇔A(g)+C(g) , and Y(s)⇔B(g)+C(g)
At a given temperature, the pressure over excess solid X is 40mm and total pressure over solid Y is 80mm. Calculate
a. The value of Kp for two reactions.
b. The ratio of moles of A and B in the vapour state over a mixture of X and Y.
c. The total pressure of gases over a mixture of X and Y.
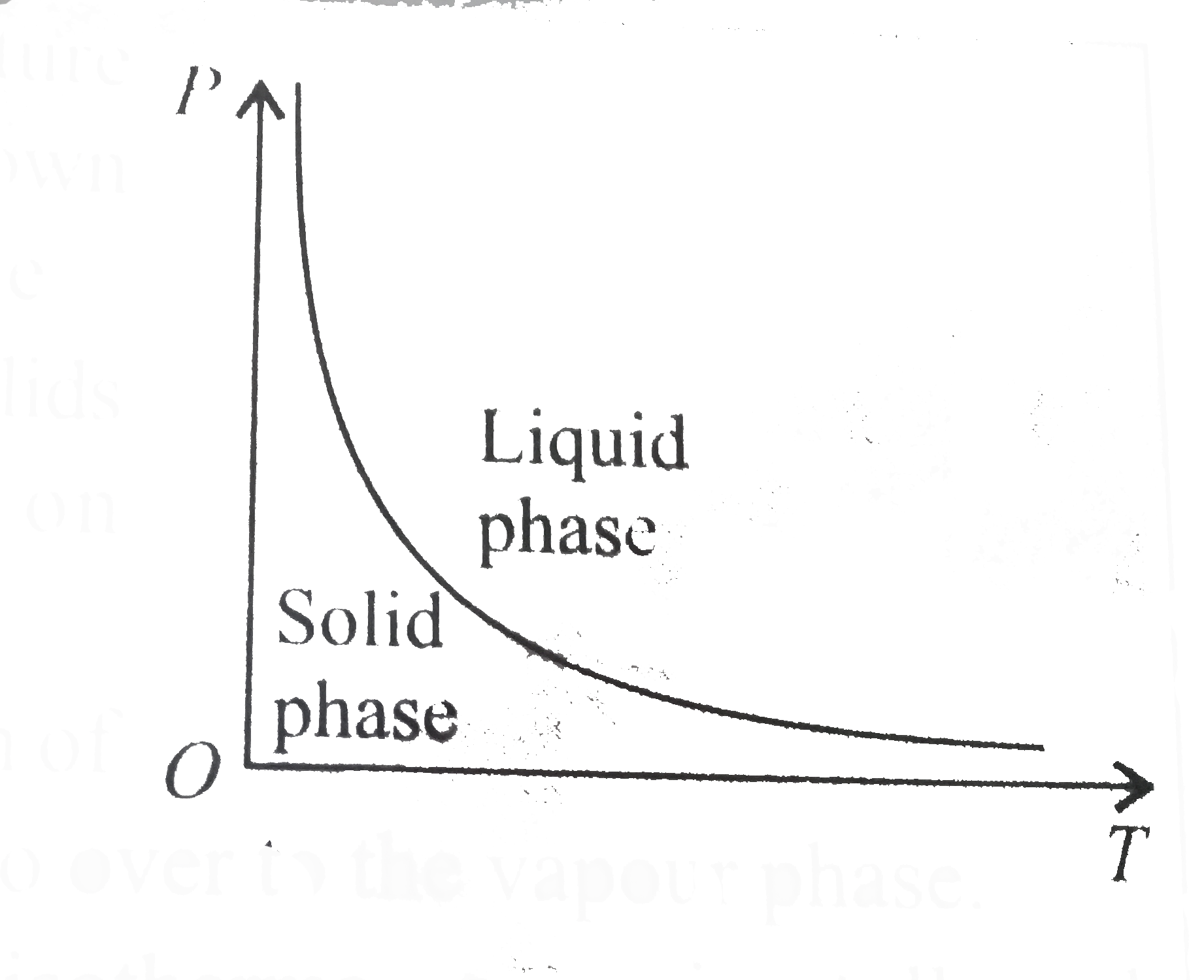
View SolutionThe pressure -temperature (P−T) phase diagram shown below corresponds to the
a. Curve of fusion of solids that expand on solidification.
b. Curve of sublimation of solides that directly go over to the vapour phase.
View Solution
