Let a three-dimensional vector →V satisfies the conditions, 2→V+(ˆi+2ˆj)×→V=2ˆi+ˆk. If 3∣∣→V∣∣=√m, then find the value of m.
The correct Answer is:6
Step by step video, text & image solution for Let a three-dimensional vector vecV satisfies the conditions, 2vecV + (hati + 2hatj) xx vecV = 2hati +hatk. If 3|vecV|=sqrt(m), then find the value of m. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
If the vectors 2ˆi−3ˆj+4ˆkandˆi+2ˆj−ˆkandmˆi−ˆj+2ˆk are coplanar, then the value of m is
A58B85C−74D23 - Question 2 - Select One
If the vectors 2ˆi−3ˆj+4ˆkandˆi+2ˆj−ˆkandmˆi−ˆj+2ˆk are coplanar, then the value of m is
A58B85C−74D23 - Question 3 - Select One
A particle moves in plane with acceleration →a=2ˆi+2ˆj. If →v=3ˆi+6ˆj, then final velocity of particle at time t=2s is
A5ˆi+8ˆjB7ˆi+10ˆjC2ˆi+6ˆjD3ˆi+2ˆj
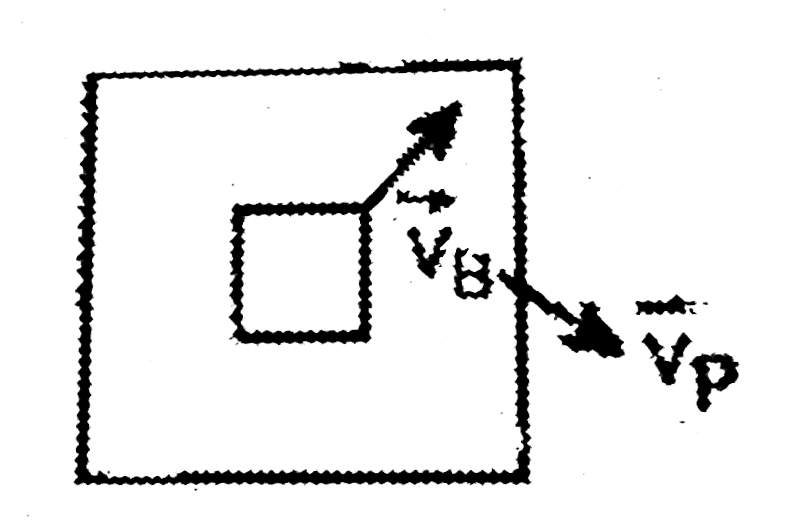
Find unit vector in direction of friction force acting on block
→vp=7ˆi−2ˆj,→vB=3ˆi+ˆj
 View Solution
View SolutionThe velocity (in m/s) of an object changes from →v1=10ˆi+4ˆj+2ˆkto→v2=4ˆi+2ˆj+3ˆk in 5 second. Find the magnitude of average acceleration.
View SolutionLet →uand→v be unit vectors such that →u×→v+→u=→wand→w×→u=→v . Find the value of [→u→v→w]
View SolutionIf a particle of charge 1μC is projected into a magnetic field →B=(2ˆi+yˆj–zˆk)T with a velocity →V=(4ˆi+2ˆj−6ˆk)ms−1 , then it passes undeviated. If it is now projected with a velocity →V=ˆi+ˆj , then find the force experienced by it
View SolutionTwo particles having position verctors →r1=(3ˆi+5ˆj) metres and →r2=(−5ˆi−3ˆj) metres are moving with velocities →v1=(4ˆi+3ˆj)m/sand→v2=(αˆi+7ˆj)m/s. If they collide after 2 seconds, the value of α is
View Solution

