If $I_{1}, I_{2}, I_{3}$ are the centers of escribed circles of $A B C,$ show that are of $I_{1} I_{2} I_{3} = \frac{a b c}{2 r} .$

Video Solution

|

Answer

Step by step video & image solution for If I_1, I_2, I_3 are the centers of escribed circles of A B C , show that are of I_1I_2I_3=(a b c)/(2r)dot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS TRIGONOMETRIC FUNCTIONS

Similar Questions

If $I_{1}, I_{2}, I_{3}$ are the centers of escribed circles of $Δ A B C$ , show that the area of $Δ I_{1} I_{2} I_{3}$ is (abc)/(2r)
View Solution
If 1 is the incentre and $I_{1}, I_{2}, I_{3}$ are the centre of escribed circles of the $△ A B C$ . Prove that
$I I_{1}^{2} + I_{2} I_{3}^{2} = I I_{2}^{2} + I_{3} I_{1}^{2} = I_{1} I_{2}^{2} + I I_{3}^{2}$
View Solution

Knowledge Check

The moment of inertia of thin square plate $A B C D$ of uniform thickness about an axis passing through the center $O$ and perpendicular to the plane of the plate is

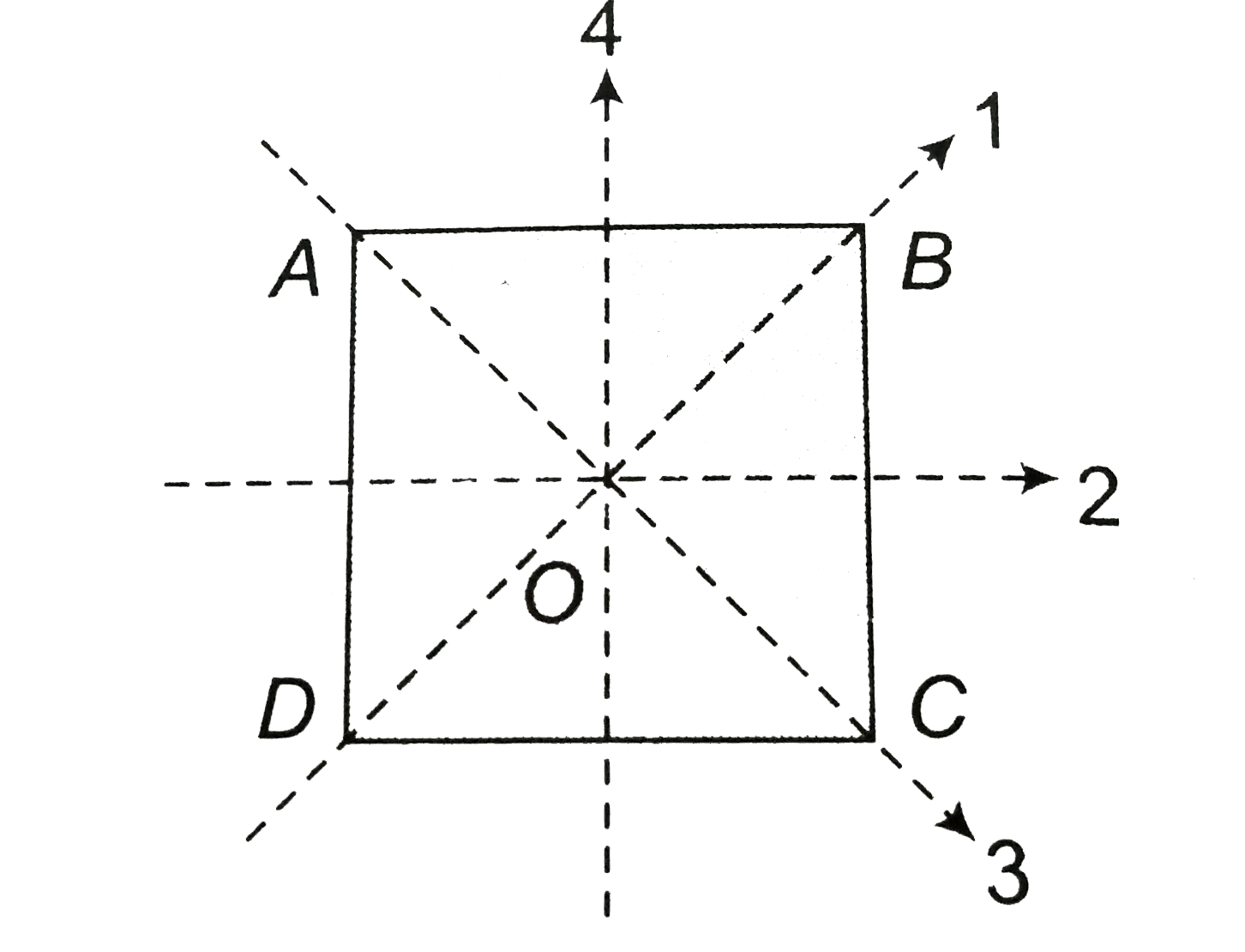
( $i$ ) $I_{1} + I_{2}$
( $i i$ ) $I_{2} + I_{4}$
( $i i i$ ) $I_{1} + I_{3}$
( $i v$ ) $I_{1} + I_{2} + I_{3} + I_{4}$
where $I_{1}$ , $I_{2}$ , $I_{3}$ and $I_{4}$ are repectively moments of inertia about axes $1$ , $2$ , $3$ and $4$ which are in the plane of the plane
A( $i$ ),( $i i$ )
B( $i$ ), ( $i i$ ), ( $i i i$ )
C( $i i$ ), ( $i i i$ )
D( $i$ ), ( $i i i$ )

Recommended Questions

Home
Ask Doubt
Profile