In the given figure, what is the radius of the inscribed circle? 32 (b) 52 (c) 75 (d) none of these
To find the radius of the inscribed circle (inradius) of the triangle with sides 3, 4, and 5, we can follow these steps:
Step 1: Identify the triangle and its properties
We have a right triangle with sides:
- a=3
- b=4
- c=5
Step 2: Calculate the area of the triangle
The area A of a right triangle can be calculated using the formula:
A=12×base×height
Here, we can take a=3 as the base and b=4 as the height:
A=12×3×4=6
Step 3: Calculate the semi-perimeter of the triangle
The semi-perimeter s is given by:
s=a+b+c2=3+4+52=122=6
Step 4: Use the formula for the radius of the inscribed circle
The radius r of the inscribed circle can be calculated using the formula:
r=As
Substituting the values of A and s:
r=66=1
Step 5: Verify the calculation
We can also verify by using the formula for the area in terms of the inradius:
A=r×s
Substituting the values we have:
6=r×6⟹r=1
Conclusion
Thus, the radius of the inscribed circle is r=1.
Final Answer
The answer is not listed in the options provided (a) 32, (b) 52, (c) 75, (d) none of these. Therefore, the correct choice is (d) none of these.
---
We have a right triangle with sides:
- a=3
- b=4
- c=5
The area A of a right triangle can be calculated using the formula:
A=12×base×height
Here, we can take a=3 as the base and b=4 as the height:
A=12×3×4=6
The semi-perimeter s is given by:
s=a+b+c2=3+4+52=122=6
The radius r of the inscribed circle can be calculated using the formula:
r=As
Substituting the values of A and s:
r=66=1
We can also verify by using the formula for the area in terms of the inradius:
A=r×s
Substituting the values we have:
6=r×6⟹r=1
Thus, the radius of the inscribed circle is r=1.
The answer is not listed in the options provided (a) 32, (b) 52, (c) 75, (d) none of these. Therefore, the correct choice is (d) none of these.
Similar Questions
Knowledge Check
In the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?
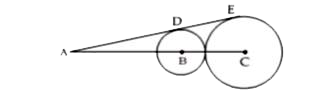 A3√15B5√15C6√15D4√15
A3√15B5√15C6√15D4√15
Which of the following is a proper fraction? 35 (b) 53 (c) 123 (d) None of these
View SolutionIf in a triangle, the area is numerically equal to the perimeter, then the radius of the inscribed circle of the triangle is (a) 1 (b) 1.5 (c) 2 (d) 3
View Solution9.02−5.7= ? 3.32 (b) 3.23 (d) 2.32 (d) None of these
View SolutionIn the given figure, PQR is a quadrant whose radius is 7 cm. A circle is inscribed in the quadrant as shown in the figure. What is the area (in cm2) of the circle

View SolutionThe diameter of a circle is 3.5 cm. What is the circumference of the circle? (a) 11 cm (b) 22 cm (c) 38.5 cm (d) 45.2 cm (e) None of these
View SolutionIf 25a+25b=115 , what is the average of a and b ? (a) 2.5 (b) 3.4 (c) 4.5 (d) 4.6 (e) None of these
View SolutionIn the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?

View Solution
