Let →C=→A+→B then :
∣∣→C∣∣ is always greater then ∣∣→A∣∣ and ∣∣→C∣∣<∣∣→B∣∣
it is possible to have
∣∣→C∣∣ is always equal to ∣∣→A+→B∣∣
∣∣→C∣∣ is never equal to ∣∣→A+→B∣∣
The correct Answer is:bc
To solve the question →C=→A+→B, we will analyze the vector addition using the triangle law of vector addition.
1. Understanding Vector Addition:
- The equation →C=→A+→B indicates that vector C is the resultant of vectors A and B.
- According to the triangle law of vector addition, if you place vector A and vector B such that the tail of vector B is at the head of vector A, the resultant vector C will be drawn from the tail of vector A to the head of vector B.
2. Visual Representation:
- Draw vector A and vector B such that they are connected head-to-tail. This means you start from the tail of vector A and draw vector B from the head of vector A.
- The resultant vector C will be represented as the line connecting the tail of A to the head of B.
3. Magnitude of Vectors:
- The magnitude of a vector is its length. Let's denote:
- |A| = magnitude of vector A
- |B| = magnitude of vector B
- |C| = magnitude of vector C
- According to the triangle inequality, the magnitude of the resultant vector C must satisfy the following conditions:
- |C| < |A| + |B| (the sum of the lengths of any two sides of a triangle is greater than the length of the third side)
- |C| can be equal to |A| + |B| only when vectors A and B are in the same direction.
4. Conclusion:
- From the triangle law, we conclude that:
- |C| is always less than or equal to |A| + |B|.
- |C| can never be greater than |A| + |B|, and it can be equal only when A and B are collinear and in the same direction.
- Therefore, the correct statements regarding the relationship between the magnitudes of these vectors are:
- |C| < |A| + |B|
- |C| = |A| + |B| (only when A and B are in the same direction)
- |C| > |A| is not always true.
Summary of Correct Options:
- The correct options based on the analysis are:
- |C| < |A| + |B|
- |C| = |A| + |B| (under specific conditions)
- The equation →C=→A+→B indicates that vector C is the resultant of vectors A and B.
- According to the triangle law of vector addition, if you place vector A and vector B such that the tail of vector B is at the head of vector A, the resultant vector C will be drawn from the tail of vector A to the head of vector B.
- Draw vector A and vector B such that they are connected head-to-tail. This means you start from the tail of vector A and draw vector B from the head of vector A.
- The resultant vector C will be represented as the line connecting the tail of A to the head of B.
- The magnitude of a vector is its length. Let's denote:
- |A| = magnitude of vector A
- |B| = magnitude of vector B
- |C| = magnitude of vector C
- According to the triangle inequality, the magnitude of the resultant vector C must satisfy the following conditions:
- |C| < |A| + |B| (the sum of the lengths of any two sides of a triangle is greater than the length of the third side)
- |C| can be equal to |A| + |B| only when vectors A and B are in the same direction.
- From the triangle law, we conclude that:
- |C| is always less than or equal to |A| + |B|.
- |C| can never be greater than |A| + |B|, and it can be equal only when A and B are collinear and in the same direction.
- Therefore, the correct statements regarding the relationship between the magnitudes of these vectors are:
- |C| < |A| + |B|
- |C| = |A| + |B| (only when A and B are in the same direction)
- |C| > |A| is not always true.
- The correct options based on the analysis are:
- |C| < |A| + |B|
- |C| = |A| + |B| (under specific conditions)
Similar Questions
At what angle the two force →A+→B and →A−→B act so that their resultant is √3A2+B2 ?
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R The distance between the point P and S is ∣∣→R∣∣ . The general relation among vectors →P,→Q and →S is :
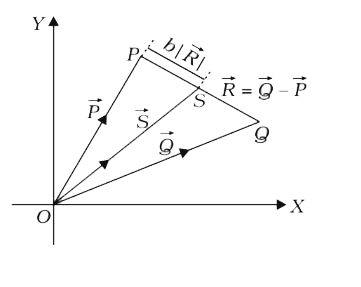
View Solution
Knowledge Check
Dot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means →A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
→A=ˆi+ˆj−ˆk and →B=2ˆi+3ˆj+5ˆk angle between →A and →B isA120∘B90∘C60∘D30∘If ∣∣→A−→B∣∣=∣∣→A∣∣−∣∣→B∣∣ the angle between →A and →B is
A60∘B0∘C120∘D90∘The maqunitudes of vecotr →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is :
A0BπCπ/2Dπ/4
If ∣∣→A+→B∣∣=∣∣→A−→B∣∣ what is the angle between →A and →B ?
View SolutionABCDEF is regular hexagon with point O as centre. The value of →AB+→AC+→AD+→AE+→AFn×→AO is . Find n.
View SolutionDot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means ovsert(→)A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
For non zero vectors →A,→B,→C,∣∣(→A×→B).→C∣∣=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣ holds if and only if
View SolutionChoose the correct symbols :
RNAa−−→DNAb−−→DNAc−−→mRNAd−−→ Polypeptide
View SolutionThe angle between vector (→A×→B) and (→B×→A) is :
View Solution
