A spherical ball is placed between a vertical wall and a movable inclined plane as shown. There is no friction between the wall and the ball, and no friction between the ball and the inclined plane. The coefficient of friction between the inclined plane and the ground is The system is in equilibrium.
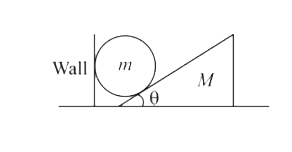
The minimum value of μ is :
mtanθM+m
mcosθM+m
mtanθM+msinθ∞cosθ
msinθM+mcos2θ
The correct Answer is:a
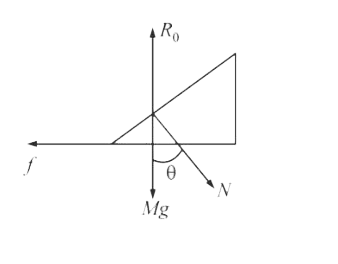
Friction acts on the incline to balance the horizontal component of Balancing forces on incline,
R0=Mg+Ncosθ→R0=(M+m)g
Nsinθf→f=Nsinθmgtanθ
Now put f=μR0 to get
μ=mtanθM+m
This is the minimum value of μ
Similar Questions
A spherical ball is placed between a vertical wall and a movable inclined plane as shown. There is no friction between the wall and the ball, and no friction between the ball and the inclined plane. The coefficient of friction between the inclined plane and the ground is The system is in equilibrium.

The normal force exerted by the plane on the ball isView SolutionThe coefficient of friction between the block and the inclined plane is μ.
View Solution
Knowledge Check
- Question 1 - Select One
A rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the incline,d plane. Then body:
 AA rollsBA does not experience any frictionCA and B has equal acceleration and unequal velocitiesDA rolls depending upon the angle of inclination θ
AA rollsBA does not experience any frictionCA and B has equal acceleration and unequal velocitiesDA rolls depending upon the angle of inclination θ - Question 2 - Select One
A rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the inclined plane. Then body:
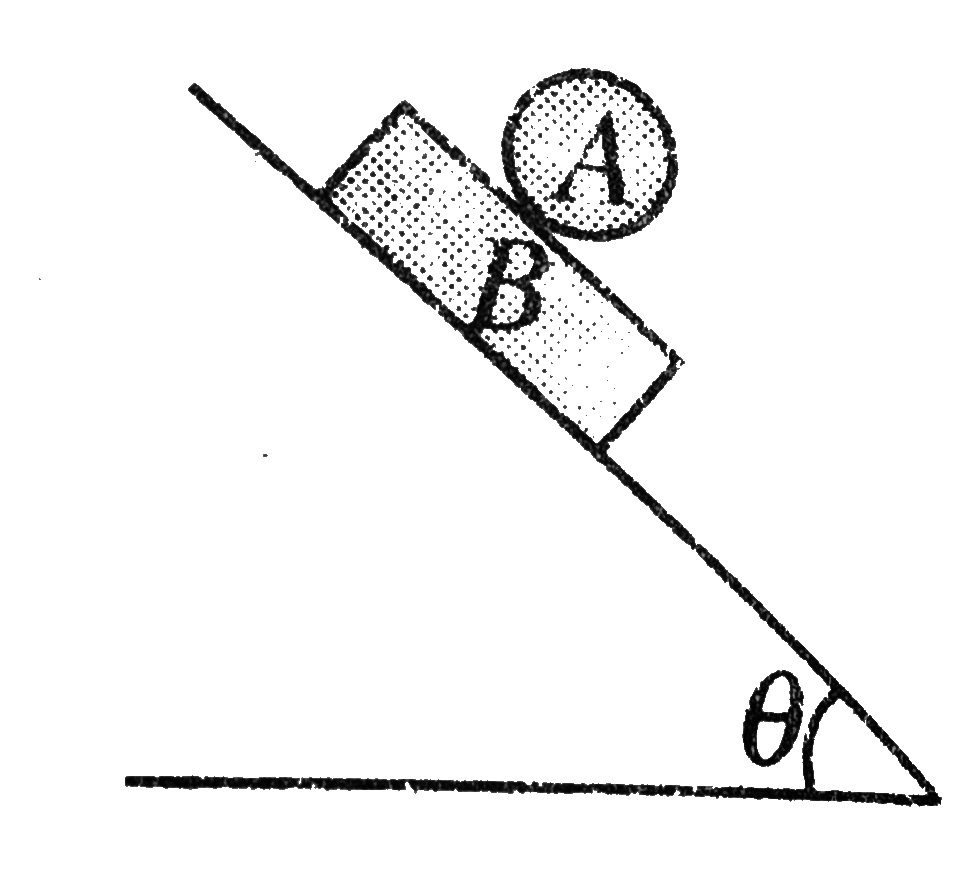 AA rollsBdoes not experience any frictionCA and B has equal acceleration and unequal velocitiesDA rolls depending upon the angle of inclination θ
AA rollsBdoes not experience any frictionCA and B has equal acceleration and unequal velocitiesDA rolls depending upon the angle of inclination θ - Question 3 - Select One
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A ball of mass M is in equilibrium between a vertical wall and the inclined surface of a wedge. The inclination of the wedge is θ=45∘ and its mass is very small compared to that of the ball. The coefficient of friction between the wedge and the floor is μ and there is no friction elsewhere. Find minimum value of μ for which this equilibrium is possible
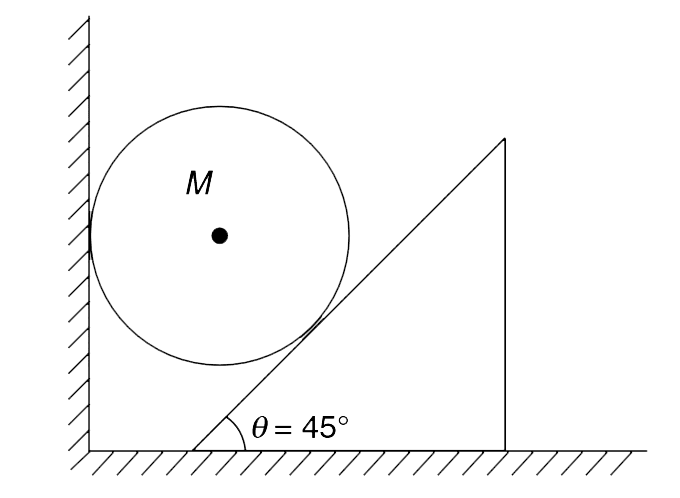 View Solution
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution

