If a cell of constant $E . M . F .$ produces the same amount of the heat during the same time in two independent resistors $R_{1}$ and $R_{2}$ , when they are separately connected across the terminals of the cell, one after the another, find the internal resistance of the cell.

Video Solution

Text Solution

Verified by Experts

$\sqrt{R_{1} R_{2}}$

v31
A $\frac{2 (E - V) V}{r}$
B $\frac{2 (E - V) r}{E}$
C $\frac{(E - V) r}{V}$
D $(E - V) r$
Null point in the galvanometer is obtained when a cell of emf E and internal resisance r is connncted across the length of 22 cm wire of the potentiometer . Now a resistane of $10 Ω$ is connected across the terminals of the cell (by closing the key K) and null point is obtained against the length of cm. The internal resistance r of the cell is -

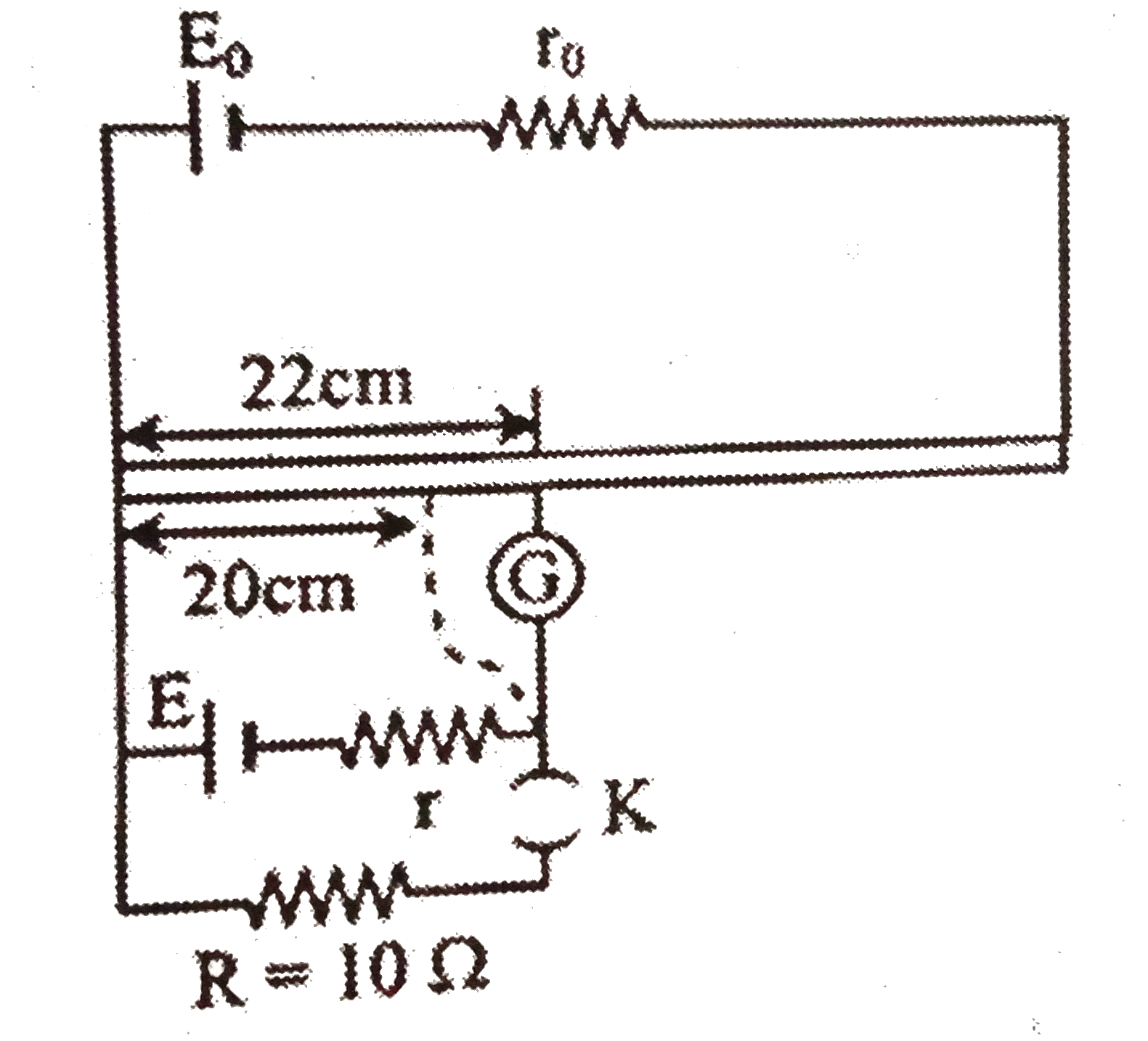A $0.5 Ω$
B $1 Ω$
C $1.5 Ω$
D $2 Ω$
A cell of e.m.f E is connected to a resistance $R_{1}$ for time i and the amount of heat generated in it is H. If the resistance $R_{1}$ is replaced by another resistance $R_{2}$ and is connected to the cell for the same time i, the amount of heat generated in $R_{2}$ is 4H. Then the internal resistance of the cell is
A $\frac{2 R_{1} + R_{2}}{2}$
B $\sqrt{R_{1} R_{2}} \frac{2 \sqrt{R_{2}} - \sqrt{R_{1}}}{\sqrt{R_{2}} - 2 \sqrt{R_{1}}}$
C $\sqrt{R_{1} R_{2}} \frac{\sqrt{R_{2}} - 2 \sqrt{R_{1}}}{2 \sqrt{R_{2}} - \sqrt{R_{1}}}$
D $\sqrt{R_{1} R_{2}} \frac{\sqrt{R_{2}} - 2 \sqrt{R_{1}}}{2 \sqrt{R_{2}} + \sqrt{R_{1}}}$