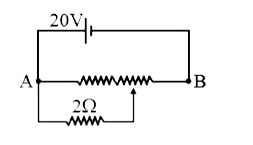
A triangle is constructed using the wires AB,BC and CA of same material and of resistance α,2α and 3α respectively. Another wire of resistance α/3 from A can make a sliding contact with wire BC. Find the maximum resistance of the network between point A and the point of sliding wire with BC.
(3/11)α
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION E- Electrical Power & Energy3videos
CURRENT ELECTRICITY
- BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION F- Electrical Instrument + Exp. Verifying ohm s law & Specific Resistance Using Meter Brige & post Office + Potentiometer (EMF & Int Res.)3videos
CURRENT ELECTRICITY
- BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION B- Resistance & resistivity ,Ohms law +VI (Volt - Curr.) Characteristics + Colour Code + Temp . Dependence6videos
CURRENT ELECTRICITY
- BOOK - MOTIONCHAPTER - CONSTRAINED MOTION EXERCISE - EXAMPLES12videos
CONSTRAINED MOTION
- BOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -360videos
ELASTICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Temperature coefficient of resistance α and resistivity ρ of a potentiometer wire must be
Ahigh and lowBlow and highClow and lowDhigh and high - Question 2 - Select One
A wire is bent in the form of a triangle now the equivalent resistance between its one end and the mid point of the side is
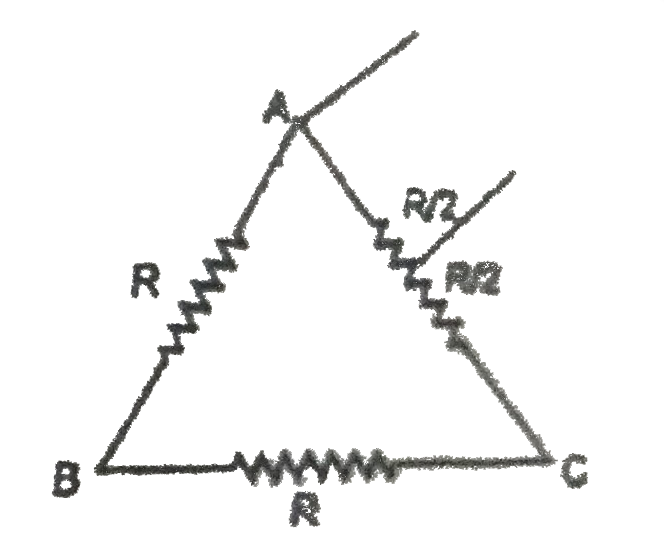 A5R12B7R12C3R12DR12
A5R12B7R12C3R12DR12 - Question 3 - Select One
A uniform wire of resistance 9Ω is joined end-to-end to from a circule. Then, the resistance of the circular wire between any two diametrically points is
A6ΩB3ΩC94ΩD32Ω
If the sides AB, BC and CA of a triangle ABC have 3, 5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices, is equal to :
View SolutionA tower subtends angles α,2αand3α respectively at points, A, B and C (all points lying on the same side on a horizontal line through the foot of the tower), then the value of ABBC is equal to
View SolutionFour wires AB , BC , CD , DA of resistance 4 ohm each and a fifth wire BD of resistance 8 ohm are joined to form a rectangle ABCD of which BD is a diagonal. The effective resistance between the points A and B is
View SolutionThere is an infinite wire grid with cells in the form of equilateral triangles. The resistance of each wire between neighboring joint connections is R0 The net resistance of the whole grid between the points A and B as shown in fig.
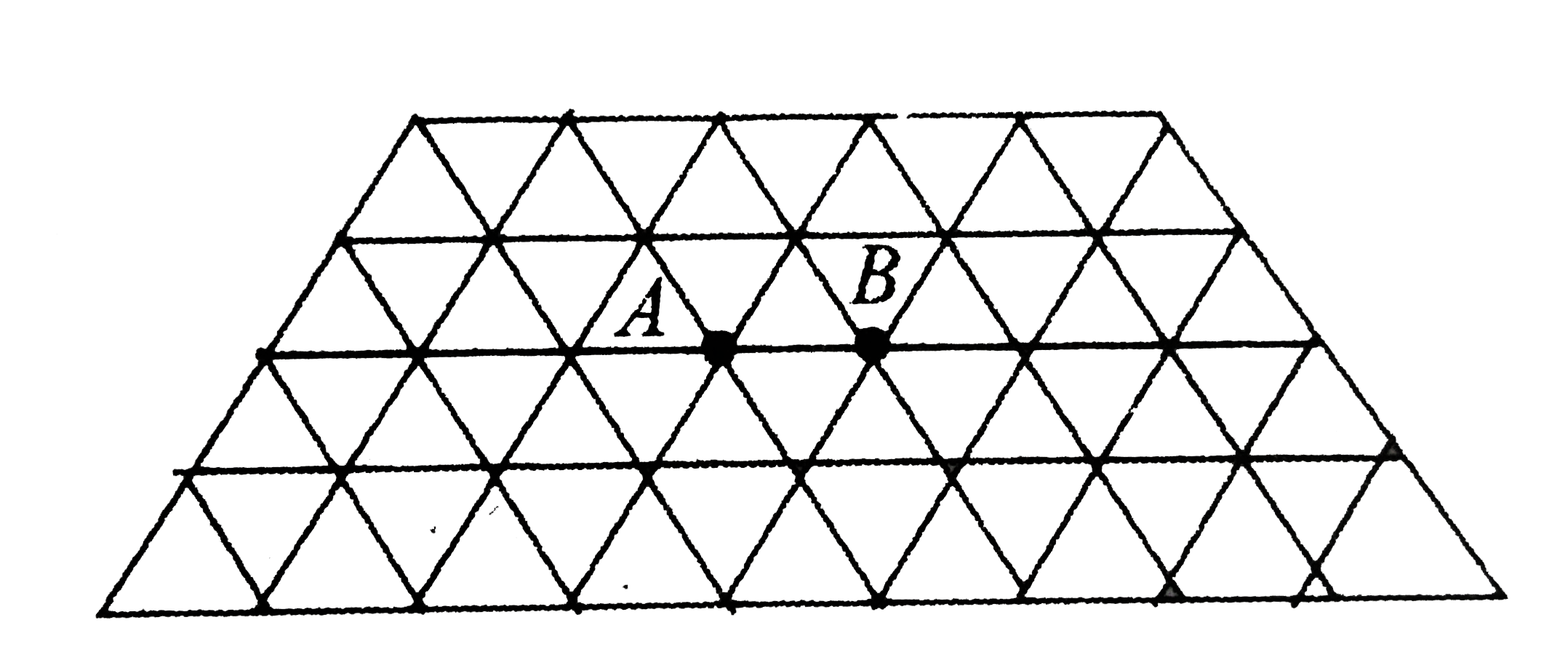 View Solution
View SolutionThe sides AB, BC, CA, of a triangle ABC have 3, 4 and 5 interior points respectively on them. The total number of triangles that can be constructed by using these points as vertices is
View Solution