A spherical shell has a radius of 1.90 m. An applied torque of 960 N-m gives the shell an angular acceleration of 6.20 rad/s2 about an axis passing through the centre of the shell. What are
the mass of the shell ?
To find the mass of the spherical shell, we can follow these steps:
Step 1: Use the relationship between torque, moment of inertia, and angular acceleration.
The formula relating torque (τ), moment of inertia (I), and angular acceleration (α) is given by:
τ=I⋅α
Where:
- τ = torque (in N·m)
- I = moment of inertia (in kg·m²)
- α = angular acceleration (in rad/s²)
Step 2: Rearrange the formula to find the moment of inertia (I).
From the equation above, we can express moment of inertia as:
I=τα
Step 3: Substitute the given values into the equation.
We know:
- τ = 960 N·m
- α = 6.20 rad/s²
Substituting these values into the equation:
I=960N⋅m6.20rad/s2
Step 4: Calculate the moment of inertia (I).
Perform the calculation:
I=9606.20≈154.84kg⋅m2
Step 5: Use the formula for the moment of inertia of a spherical shell.
The moment of inertia (I) for a thin spherical shell is given by:
I=23mr2
Where:
- m = mass of the shell (in kg)
- r = radius of the shell (in m)
Step 6: Rearrange the formula to find the mass (m).
Rearranging the formula gives:
m=3I2r2
Step 7: Substitute the values of I and r into the equation.
We have:
- I ≈ 154.84 kg·m²
- r = 1.90 m
Substituting these values:
m=3×154.842×(1.90)2
Step 8: Calculate the mass (m).
Perform the calculation:
1. Calculate (1.90)2=3.61
2. Now substitute:
m=3×154.842×3.61=464.527.22≈64.4kg
Final Answer:
The mass of the spherical shell is approximately 64.4 kg.
---
The formula relating torque (τ), moment of inertia (I), and angular acceleration (α) is given by:
τ=I⋅α
Where:
- τ = torque (in N·m)
- I = moment of inertia (in kg·m²)
- α = angular acceleration (in rad/s²)
From the equation above, we can express moment of inertia as:
I=τα
We know:
- τ = 960 N·m
- α = 6.20 rad/s²
I=960N⋅m6.20rad/s2
Perform the calculation:
I=9606.20≈154.84kg⋅m2
The moment of inertia (I) for a thin spherical shell is given by:
I=23mr2
Where:
- m = mass of the shell (in kg)
- r = radius of the shell (in m)
Rearranging the formula gives:
m=3I2r2
We have:
- I ≈ 154.84 kg·m²
- r = 1.90 m
m=3×154.842×(1.90)2
Perform the calculation:
1. Calculate (1.90)2=3.61
2. Now substitute:
m=3×154.842×3.61=464.527.22≈64.4kg
The mass of the spherical shell is approximately 64.4 kg.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
A spherical shell has a radius of 1.90 m. An applied torque of 960 N-m gives the shell an angular acceleration of 6.20 rad/s2 about an axis passing through the centre of the shell. What are
the rotational inertia of the shell about that axis
View SolutionAn element has 2 electrons in the M shell. What is the atomic number of the element ?
View Solution
Knowledge Check
Three idential spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
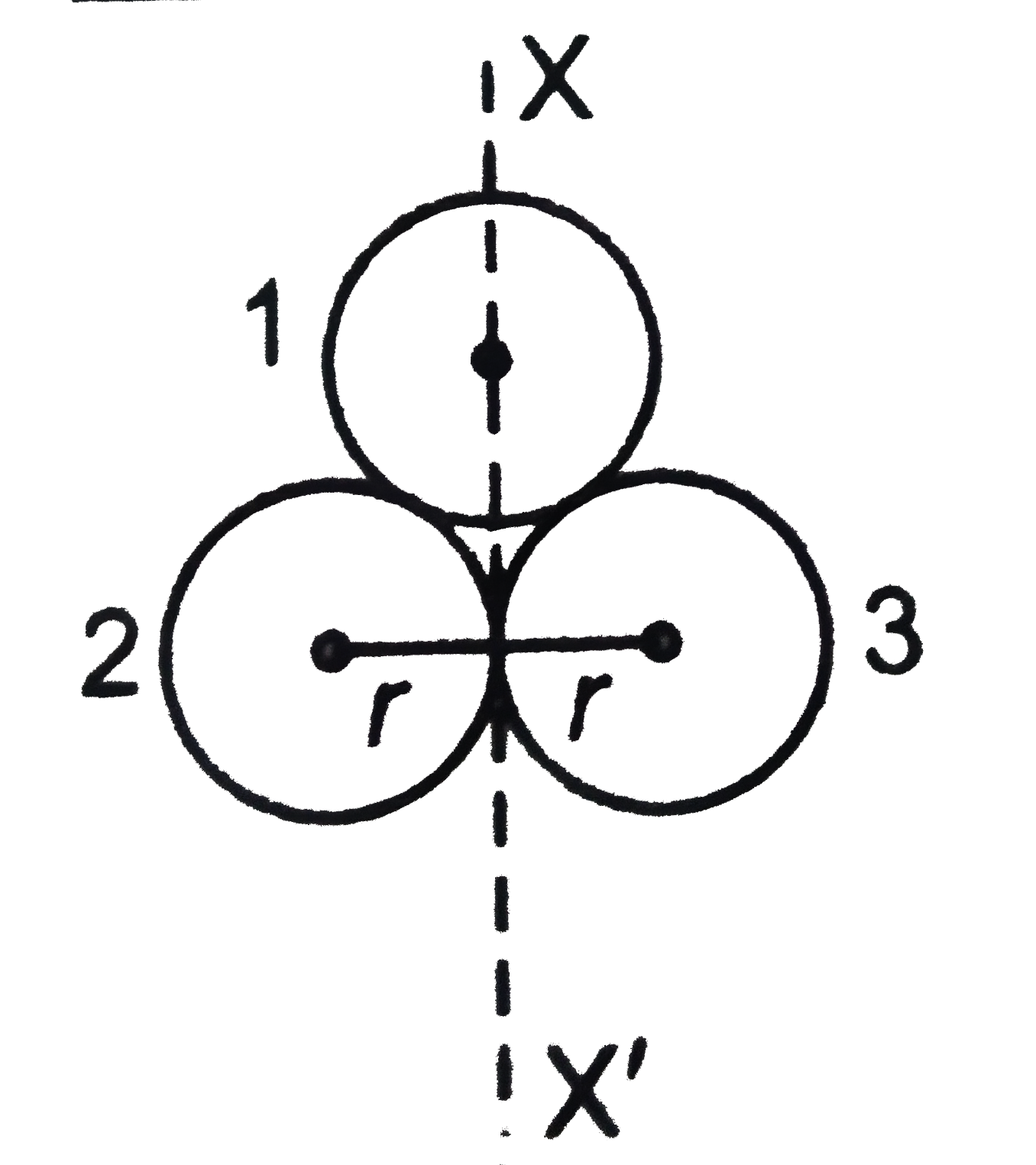 A3mr2B165mr2C4mr2D115mr2
A3mr2B165mr2C4mr2D115mr2A particle of mass m is placed inside a spherical shell, away from its centre. The mass of the shell is M.
AThe particle will move towards the centre.BThe particle will move away from the centre, towards the nearest wall.CThe particle will move towards the centres if m<M, and away from the centre if m>M.DThe particle will remain stationary.A point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroDGMMR2
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q:
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero even if the shell is not spherical, but has any irregular shape? Explain.
View SolutionA thin spherical shell of total mass M and radius R is held fixed. There is a small hole in the shell. A mass m is released from rest a distance R from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. How long does the mass take to travel from the hole to the point diametrically opposite.
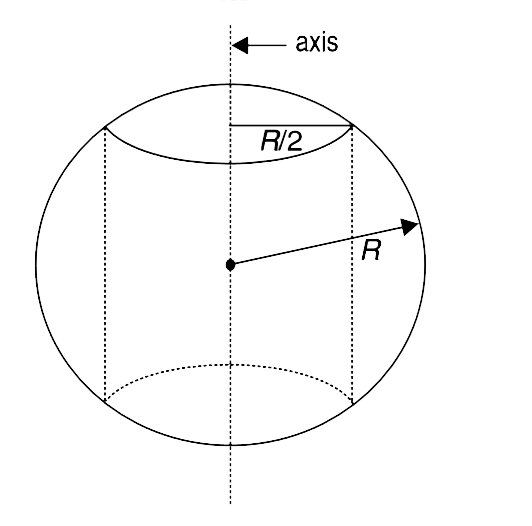
View SolutionA thin uniform spherical shell of radius R is bored such that the axis of the boring rod passes through the centre of the sphere. The boring rod is a cylinder of radius R2. Take the mass of the sphere before boring to be M.
(a) Find the mass of the leftover part
(b) Find the moment of inertia of the leftover part about the axis shown.
View SolutionA shell leaves the barrel of a gun at a speed of 800 m/s. The barrel is 2.0 m long. Find the average acceleration.
View Solution
