A solid cylinder of mass 'M' and radius 'R' is rotating along its axis with angular velocity ω without friction. A particle of mass 'm' moving with velocity v collides aganist the cylinder and sticks to its rim. After the impact calculate angular velocity of cylinder .
To solve the problem, we will use the principle of conservation of angular momentum. Here are the steps to find the angular velocity of the cylinder after the particle sticks to its rim.
Step 1: Identify the initial angular momentum of the system
The initial angular momentum of the solid cylinder can be calculated using the formula:
Linitial=Icylinder⋅ω
where Icylinder is the moment of inertia of the solid cylinder, given by:
Icylinder=12MR2
Thus, the initial angular momentum of the cylinder is:
Linitial=12MR2⋅ω
Step 2: Calculate the angular momentum of the particle
The particle of mass m moving with velocity v strikes the rim of the cylinder. The angular momentum of the particle about the axis of rotation is given by:
Lparticle=m⋅v⋅R
Step 3: Write the total initial angular momentum
The total initial angular momentum of the system (cylinder + particle) before the collision is:
Ltotal_initial=Linitial+Lparticle
Substituting the expressions from Steps 1 and 2:
Ltotal_initial=12MR2⋅ω+m⋅v⋅R
Step 4: Determine the final angular momentum after the collision
After the collision, the particle sticks to the rim of the cylinder. The new angular velocity is denoted as ω′. The moment of inertia of the combined system (cylinder + particle) is:
Itotal=Icylinder+Iparticle=12MR2+mR2
Thus, the final angular momentum of the system is:
Ltotal_final=Itotal⋅ω′=(12MR2+mR2)⋅ω′
Step 5: Apply the conservation of angular momentum
According to the conservation of angular momentum:
Ltotal_initial=Ltotal_final
So we have:
12MR2⋅ω+m⋅v⋅R=(12MR2+mR2)⋅ω′
Step 6: Solve for the new angular velocity ω′
Rearranging the equation to solve for ω′:
ω′=12MR2⋅ω+m⋅v⋅R12MR2+mR2
Final Answer
The angular velocity of the cylinder after the particle sticks to its rim is:
ω′=12MR2⋅ω+m⋅v⋅R12MR2+mR2
---
The initial angular momentum of the solid cylinder can be calculated using the formula:
Linitial=Icylinder⋅ω
where Icylinder is the moment of inertia of the solid cylinder, given by:
Icylinder=12MR2
Thus, the initial angular momentum of the cylinder is:
Linitial=12MR2⋅ω
The particle of mass m moving with velocity v strikes the rim of the cylinder. The angular momentum of the particle about the axis of rotation is given by:
Lparticle=m⋅v⋅R
The total initial angular momentum of the system (cylinder + particle) before the collision is:
Ltotal_initial=Linitial+Lparticle
Substituting the expressions from Steps 1 and 2:
Ltotal_initial=12MR2⋅ω+m⋅v⋅R
After the collision, the particle sticks to the rim of the cylinder. The new angular velocity is denoted as ω′. The moment of inertia of the combined system (cylinder + particle) is:
Itotal=Icylinder+Iparticle=12MR2+mR2
Thus, the final angular momentum of the system is:
Ltotal_final=Itotal⋅ω′=(12MR2+mR2)⋅ω′
According to the conservation of angular momentum:
Ltotal_initial=Ltotal_final
So we have:
12MR2⋅ω+m⋅v⋅R=(12MR2+mR2)⋅ω′
Rearranging the equation to solve for ω′:
ω′=12MR2⋅ω+m⋅v⋅R12MR2+mR2
The angular velocity of the cylinder after the particle sticks to its rim is:
ω′=12MR2⋅ω+m⋅v⋅R12MR2+mR2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2A solid cylinder of mass 2 kg and radius 0.2m is rotating about its own axis without friction with angular velocity 3 rads/s. A particle of mass 0.5 kg and moving with a velocity 5 m/s strikes the cylinder and sticks to it as shown in figure. The angular momentum of the cylinder before collision will be?
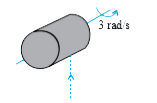 A0.12J-sB12J-sC1.2J-sD1.12J-s
A0.12J-sB12J-sC1.2J-sD1.12J-sA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
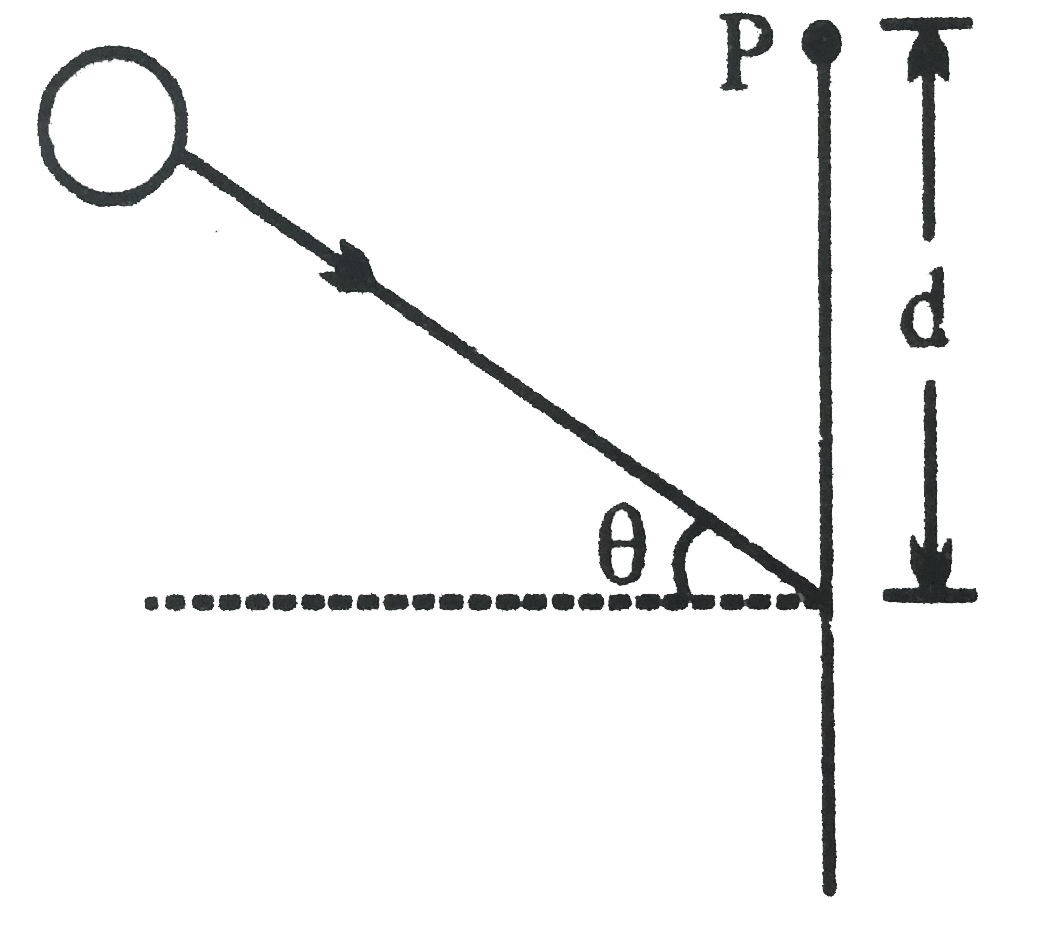 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzero
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it is
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω, Two objects, each of mass m, are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity ω=
View Solution
