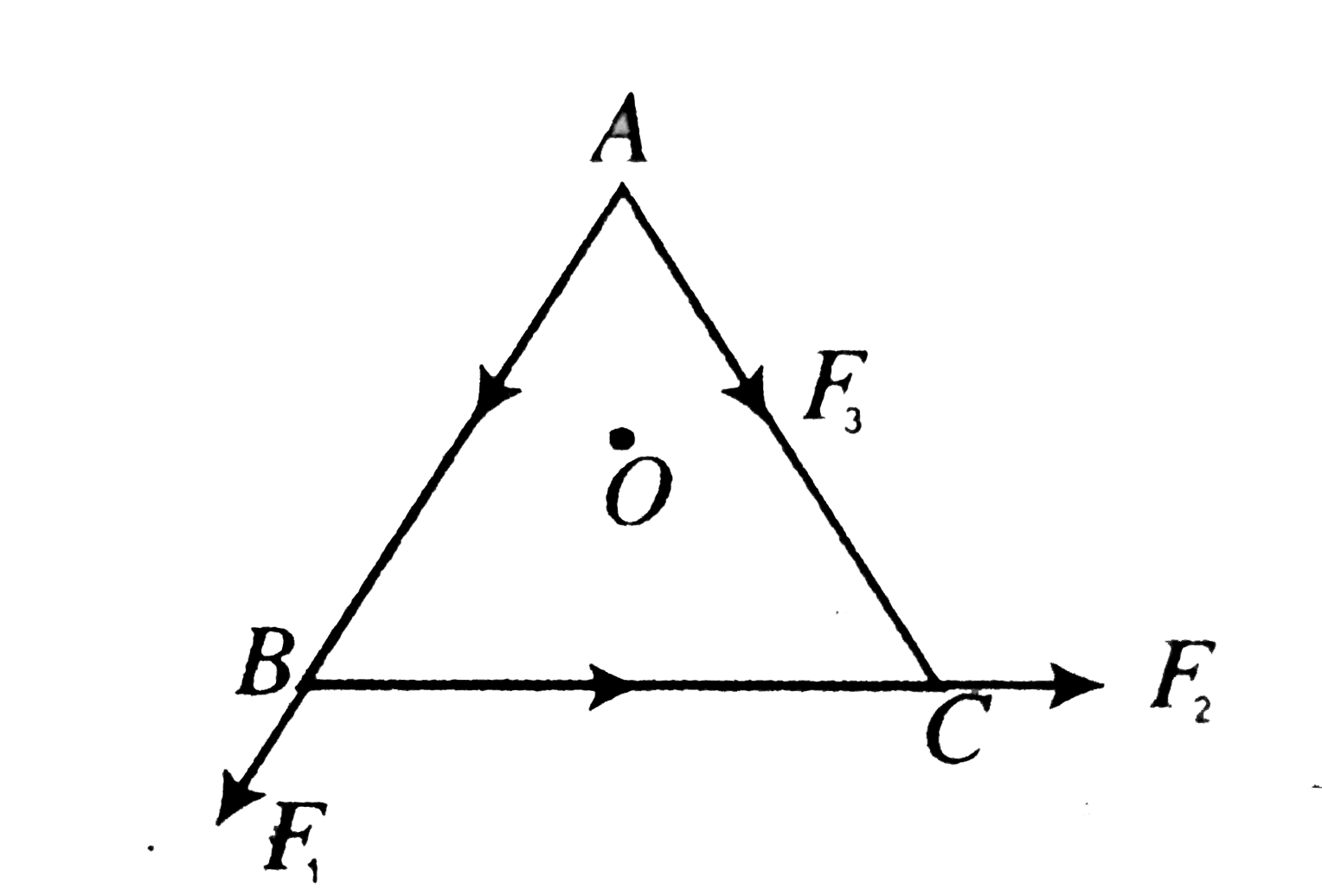
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
F1+F22
2(F2+F2)
F1+F2
F1−F2
The correct Answer is:C
Step by step video & image solution for O is the centre of an equilateral triangle ABC. F_(1), F_(2) and F_(3) are the three forces acting along the sides AB, BC and AC respectively. What should be the value of F_(3) so that the total torque about O is zero? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )
24 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
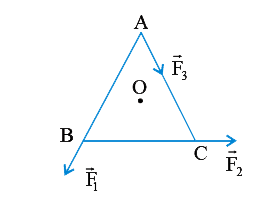
ABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
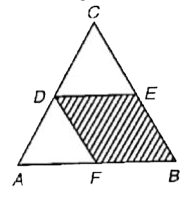
View SolutionABC is a triangle in which D, E and F are the mid-points of the sides AC, BC and AB respectively. What is the ratio of the area of the shaded to the unshaded region in the triangle?
View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
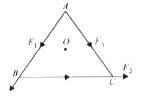 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
In the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
View SolutionGiven an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View Solution
