Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at , then prove
Video Solution
Text Solution
and are congurent
.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In an acute-angled triangle ABC, tanA+tanB+tanC
A≥3B≥√3C≥3√3Dnone of these - Question 2 - Select One
If AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEA - Question 3 - Select One
Let ABC be a triangle and O be its orthocentre .If R and R1 are the circum-radii of triangle ABC and AOB , then
AR1>RBR1=RCR1<RDnone of these
In given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
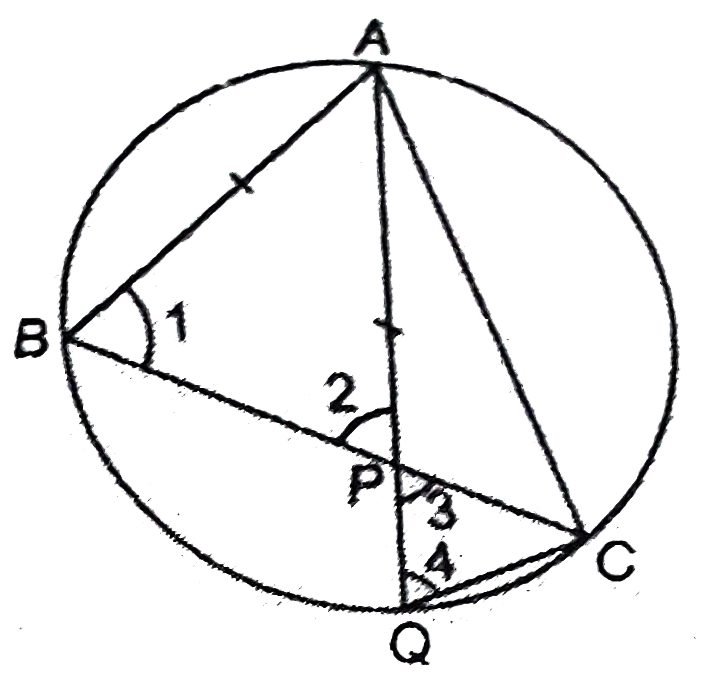 View Solution
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionIf AD, BE, CF are the altitudes of triangle ABC whose ortho centre is H then C is ortho centre of
View SolutionFind the lengths of chords of the circumcircle of triangle ABC, made by its altitudes
View SolutionLet ABC be an equilateral triangle with side length a. Let R and r denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of a, the ratio Rr
View Solution


