अर्द्ध-शक्ति बिन्दु आवृत्तियों से क्या अभिप्राय है? एक LCR श्रेणी परिपथ के लिए बैण्ड चौड़ाई ज्ञात करने का व्यंजक प्राप्त कीजिए। प्रत्यावर्ती धारा व आवृत्ति के मध्य वक्र में अर्द्धशक्ति बिन्दु आवृत्तियों को दर्शाइए।
अर्द्धशक्ति बिन्दु था आवृत्तियाँ (Half Power Points or Frequencies)चित्र में LCR श्रेणी परिपथ में आवृत्ति / परिवर्तन के साथ धारा Irms के परिवर्तन को दर्शाया गया है। अनुनाद की स्थिति में अनुनादी आवृत्ति fr पर धारा का मान अधिकतम (Irms)max होता है। इस आवृत्ति पर परिपथ में शक्ति क्षय (I2rms)max)R अधिकतम होगा। यहाँ (Irms)max अनुनाद पर प्रभावी धारा है।
अनुनादी आवृत्ति के दोनों ओर दो आवृत्तियाँ f1 और f2 पर परिपथ में शक्ति क्षय उसके अनुनादी मान का आधा होता है। इन आवृत्तियों (f1,f2) को अर्द्धशक्ति बिन्दु आवृत्तियाँ कहते हैं। वक्र के A और B बिन्दु 'अर्द्धशक्ति बिन्दु' कहलाते हैं। यदि इन बिन्दुओं पर प्रभावी धारा Irms हो तो
I2rmsR=12(Irms)2maxR
Irms=(Irms)max√2
=0.707(Irms)max
अत: अर्द्धशक्ति बिन्दुओं A और B पर धारा क-मान अधिकतम मान का 1√2 रह जाता है तथा परिपथ की शक्ति आधी रह जाती है, इन्हें अर्द्धशक्ति बिन्दु या आवृत्तियाँ कहते हैं।
बैण्ड चौड़ाई (Band Width)- अर्द्धशक्ति आवृत्तियों के मध्य आवृत्ति अन्तराल में LCR श्रेणी परिपथ स्त्रोत से अधिक ऊर्जा ग्रहण करने में समर्थ होता है। अर्द्धशक्ति आवृत्तियों के मध्य आवृत्ति अन्तराल को परिपथ की बैण्ड चौड़ाई कहते हैं। अर्थात्
बैण्ड चौड़ाई =f2−f1
अर्द्धशक्ति आवृत्तियों f1 और f2 पर
Irms=(Irms)max√2 ….(1)
Vrms√R2+(Lω−1cω)2=Vrms√2R
या R2+(Lω−1cω)2=2R2
या (Lω−1cω)2=R2
या Lω−1cω=±R ......(2)
बिंदु A के लिए Lω1−1cω1=−R ....(3)
बिंदु B के लिए Lω2−1cω2=R .....(4)
समीकरण (3) और (4) को जोड़ने पर
L(ω1+ω2)=1C(1ω1+1ω2)=0
या L(ω1+ω2)=1C(ω1+ω2ω1ω2)
या ω1ω2=1LC
इसी प्रकार समीकरण (4) में से (3) को घटाने पर
2L(ω2−ω1)+1C(1ω1−1ω2)=2R
या L(ω2−ω1)+1C(ω2−ω1ω1ω2)=2R
समीकरण (5) से ω1,ω2 का मान रखने पर
2L(ω2−ω1)=2R
(ω2−ω1)=RL ...(6)
अत: बैण्ड चौड़ाई =ω2−ω1=RL
या f2−f1=R2πL ...(7)
उपर्युक्त समीकरण (7) से बैण्ड चौड़ाई का व्यंजक प्राप्त होता है।
प्रत्यावर्ती धारा व आवृत्ति के मध्य वक्र में अर्द्धशक्ति बिन्दु की आवृत्तियाँ

Topper's Solved these Questions
- प्रत्यावर्ती धाराBOOK - SANJEEV PUBLICATIONCHAPTER - प्रत्यावर्ती धाराEXERCISE - पाठ्यपुस्तक के प्रश्न
64 Videos
- प्रकाश विद्युत प्रभाव एवं द्रव्य तरंगें BOOK - SANJEEV PUBLICATIONCHAPTER - प्रकाश विद्युत प्रभाव एवं द्रव्य तरंगें EXERCISE - उच्चस्तरीय बुद्धि-कौशल प्रश्न
9 Videos
- विद्युत चुम्बकीय प्रेरण BOOK - SANJEEV PUBLICATIONCHAPTER - विद्युत चुम्बकीय प्रेरण EXERCISE - उच्चस्तरीय बृद्धि -कौशल प्रश्न
17 Videos
Similar Questions
प्रत्यावर्ती धारा के वर्ग मध्य मूल का मान होता है -
View Solution(a) एक समोजी इलेक्ट्रॉन किरण-पुंज जिसमें इलेक्ट्रॉन की चाल 5.20×106ms−1 है, पर एक चुंबकीय क्षेत्र 1.30×10−4T किरण-पुंज की चाल के लंबवत लगाया जाता है। किरण-पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि इलेक्ट्रॉन के e/m का मान 1.76×1011Ckg−1 है?
(b) क्या जिस सूत्र को (a) में उपयोग में लाया गया है वह यहाँ भी एक 20 MeV इलेक्ट्रॉन किरण-पुंज की त्रिज्या परिकलित करने के लिए युक्त्तिपरक है? यदि नहीं तो किस प्रकार इसमें संशोधन किया जा सकता है?
View Solutionदिये गये परिपथ में अल्प प्रतिरोध R का क्या कार्य है?
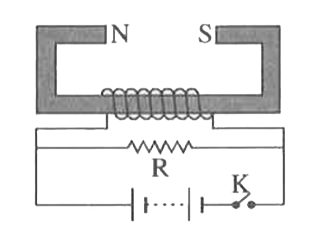
View Solutionअभ्यास 7.3 व 7.4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितने नेट शक्ति अवशोषित होती है ? अपने उत्तर का विवरण दीजिए |
7.3 : एक 44mH का प्रेरित्र 220V, 50 Hz आपूर्ति से जोड़ा गया है , परिपथ में धारा के rms मान को ज्ञात कीजिये
7.4 : एक 60μF का संधारित्र 110V, 60Hz , acआपूर्ति से जोड़ा गया है , परिपथ में धारा के rms मान को ज्ञात कीजिये
View Solutionएक श्रेणी LCR परिपथ में L=10.0H,C=40μF तथा R=60Omega को 240V वोल्ट के परिवर्ती आवृत्ति के प्रत्यावर्ती धारा स्त्रोत से जोड़ा गया है । गणना कीजिए -(i ) स्त्रोत की कोणीय आवृत्ति जो परिपथ को अनुनाद की अवस्था में लाती है ,(ii ) अनुनादी आवृत्ति पर धारा , (iii ) प्रेरक के सिरों के बीच अनुनाद की दशा में वर्ग - माध्य - मूल विभव पतन ।
View SolutionE_("rms") = 100 वोल्ट का वि. वा. बल एक LCR श्रेणी परिपथ में लगाया गया है। यदि परिपथ में प्रेरणिक प्रतिघात, धारितीय प्रतिघात तथा प्रतिरोध के मान क्रमशः 4 ओम, 12 ओम तथा 6 ओम हों तो परिपथ के लिए निम्न का मान ज्ञात कीजिए-
शक्ति गुणांक
View SolutionE_("rms") = 100 वोल्ट का वि. वा. बल एक LCR श्रेणी परिपथ में लगाया गया है। यदि परिपथ में प्रेरणिक प्रतिघात, धारितीय प्रतिघात तथा प्रतिरोध के मान क्रमशः 4 ओम, 12 ओम तथा 6 ओम हों तो परिपथ के लिए निम्न का मान ज्ञात कीजिए-
औसत शक्ति
View SolutionE_("rms") = 100 वोल्ट का वि. वा. बल एक LCR श्रेणी परिपथ में लगाया गया है। यदि परिपथ में प्रेरणिक प्रतिघात, धारितीय प्रतिघात तथा प्रतिरोध के मान क्रमशः 4 ओम, 12 ओम तथा 6 ओम हों तो परिपथ के लिए निम्न का मान ज्ञात कीजिए-
वाट-हीन धारा का वर्ग माध्य मूल मान।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionकिसी सरल रेखा से अक्षों के बीच काटे हुए अन्तः खण्ड का मध्य-बिन्दु (3,-2) है। रेखा का समीकरण ज्ञात कीजिए।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि बिन्दु (a,a) रेखाओं |2x+y|=5 के मध्य स्थित है , तब सबसे उपयुक्त एक विकल्प का चयन कीजिए|
View Solution
