A sector OABO of central angle θ is constructed in a circle with centre O and of radius 6. The radius of the circle that is circumscribed about the triangle OAB, is 6cosθ2 (b) 6secθ2 3secθ2 (d) 3(cosθ2+2)
R=abc4D
D=12⋅6⋅6sinθ
D=18sinθ
a=6,b=6
sin(θ2)=C12
C=12sin(θ2)
R=6⋅6⋅12sin(θ2)4⋅18sinθ
R=6sin(θ2)sinθ
R=3sec(θ2).
Topper's Solved these Questions
Similar Questions
A sector OABO of central angle θ is constructed in a circle with centre O and of radius 6. The radius of the circle that is circumscribed about the triangle OAB, is 6cosθ2 (b) 6secθ2 3secθ2 (d) 3(cosθ2+2)
View SolutionThe intercept made by the circle with centre (2, 3) and radius 6 on y-axis is
View Solution
Knowledge Check
- Question 1 - Select One
ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cm
find the equation of circle whose centre (−3,−2) and radius 6
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionIn the given diagram, 'O' is the centre of the circle and AC is the diameter. ∠ADB is 120∘. Radius of the circle is 6 cm, what is the area of the triangle ABC?
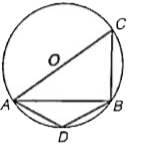 View Solution
View SolutionPoints A(−1,y) and B(5,7) lie on a circle with centre O(2,−3y). Find the values of y. Hence, find the radius of the circle.
View SolutionPoints A(−1,y) and B(5,7) lie on a circle with centre O(2,−3y) . Find the values of y. Hence, find the radius of the circle.
View SolutionThe area of a minor sector of a circle is 3.85cm2 and the measure of its central angle is 36∘. Find the radius of the circle.
View SolutionABC is an equilateral triangle of side 6 cm, a circle, centre O, passes through the vertices A, B, and C. Find the radius of the circle.
View Solution

