The limit of sum of areas of all the squares as n→∞ is (1) 2R2 (2) 3R2 (3) 4R2 (4) 8R2
Step by step video & image solution for The limit of sum of areas of all the squares as nrarr oo is (1) 2R^2 (2) 3R^2 (3) 4R^2 (4) 8R^2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
10∑r=1(4r−3)2 =
A4930B3490C9430Dnone of these - Question 2 - Select One
S=n−1∑r=01√4n2−r2as n→∞ is equal to
AπBπ8Cπ6DNone of these
limn→∞1n4n∑r=1r(r+2)(r+4)=
View Solutionli∑n−>∞n∑r=11√4n2−r2
View SolutionThe effective resistance between points P and Q of the
electrical circuit shown in the figure is
(a) 2RrR+r
(b)8R(R+r)3R+r
(c) 2r+4R
(d) 5R2+2r .
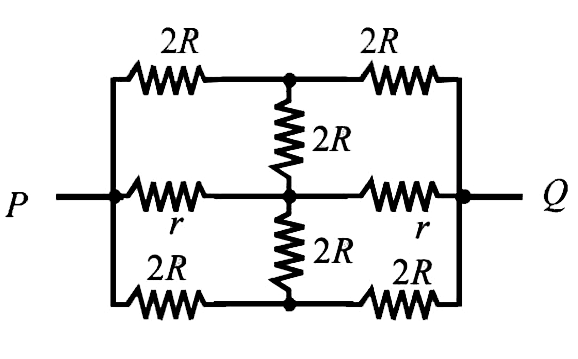 .View Solution
.View SolutionThe effective resistance between points P and Q of the
electrical circuit shown in the figure is
(a) 2RrR+r
(b)8R(R+r)3R+r
(c) 2r+4R
(d) 5R2+2r .
 .View Solution
.View SolutionIf the sum to infinity of the series 1+2r+3r2+4r3+ is 9/4, then value of r is (a)1/2 b. 1/3 c. 1/4 d. none of these
View SolutionFind the sum to n terms of the series 11+12+14+21+22+24+31+32+34+.......... that means tr=rr4+r2+1 find n∑1
View Solution

