ΔABC is an isosceles, with AB=AC. If P be any point on the side BC. Prove that AP<AB.
Step by step video & image solution for Delta ABC is an isosceles, with AB = AC. If P be any point on the side BC. Prove that AP < AB. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
ΔABC is an isosceles triangle and AB = AC. If all the sides AB. BC and CA of a ΔABC touch a circle at D, E and F respectively. Then BE is equal to :
A12 BCB13 BCC14 BCD23 BCABC is an isosceles right anlged triangle with AB = BC = 1 . If P is any point on AC, then min (max {(area APQ) , (area PQBR) , area PRC )}} is
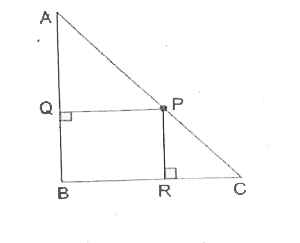 A29B19C13Dnone of these
A29B19C13Dnone of these
ABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
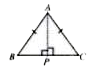
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View SolutionTriangle ABC is isosceles with AB=ACandBC=65cm. P is a point on BC such that the perpendiculardistances from P to ABandAC are 24cmand36cm, respectively. The area of triangle ABC (in sq cm is)
View SolutionIn the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
View Solution
