If √3tanθ=3sinθ then the value of (sin2θ−cos2θ) is
1
3
13
none of these
The correct Answer is:c
√3tanθ=3sinθ
shortcut method
√3sinθcosθ=3sinθ
√3cosθ=3
cosθ=√33
then perpendicular =√6
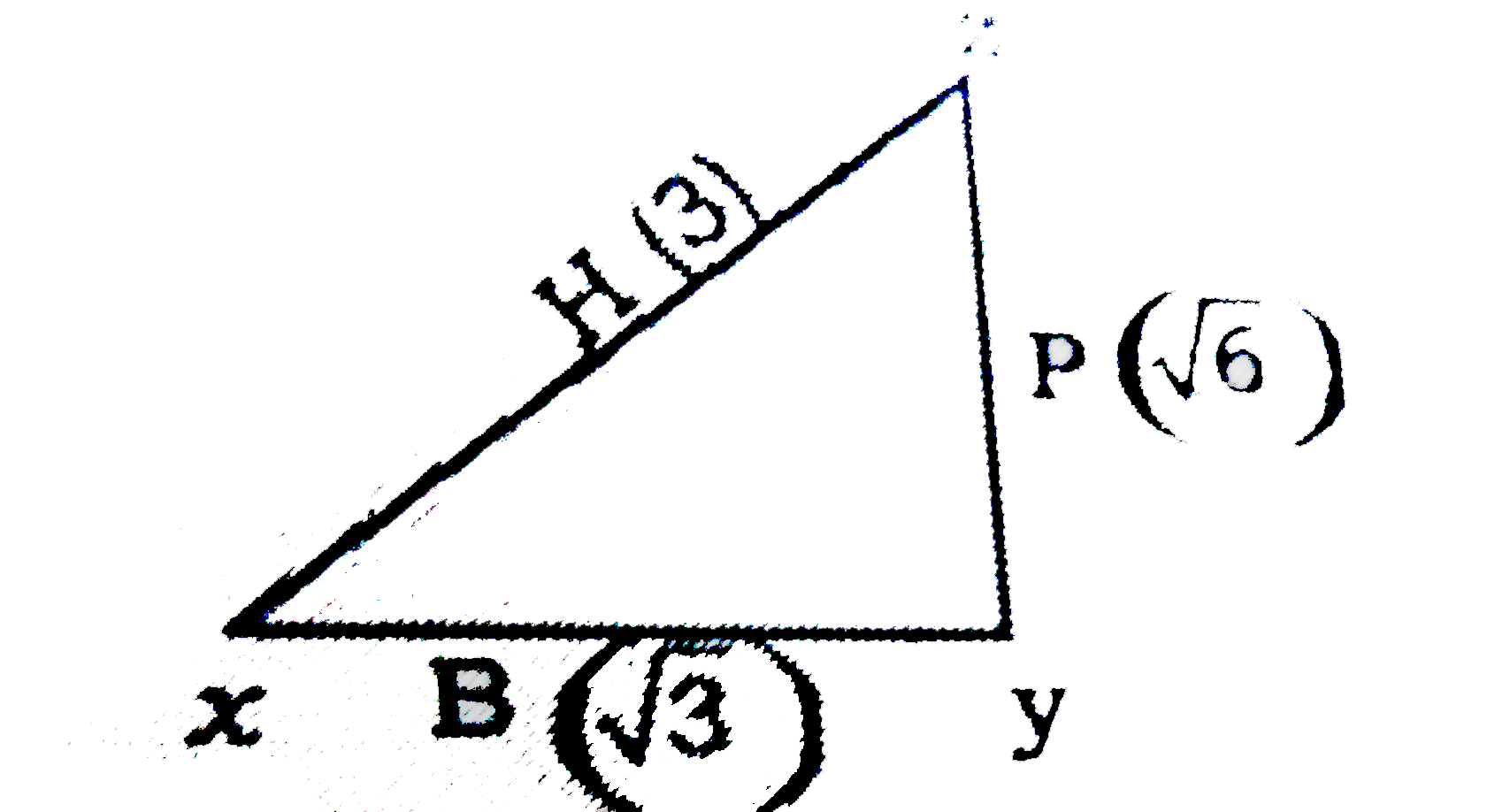
(sin2θ−cos2θ)
⇒(√6H)2−(BH)2
⇒69−39=13
Topper's Solved these Questions
Similar Questions
एक रेलगाड़ी 45 किमी. /घंटा की चाल से चल रही है उसे 4 किमी. की दूरी तय करने में लगा समय ज्ञात कीजिए ?
02:38View Solutionयदि (sinθ+cosθ)=√3, तब (tanθ+cotθ) का मान =?
04:01View Solutionसिद्ध कीजिए sinθ−2sin3θ2cos3θ−cosθ=tanθ
03:06View Solutionयदि √3tanθ=3sinθ, तब sin2θ−cos2θ का मान बराबर है -
01:42View Solutionयदि 3cosθ−4sinθ=2cosθ+sinθ तो tanθ का मान ज्ञात करो
02:12View Solutionसिद्ध कीजिए कि : sinθ−2sin3θ2cos3θ−cosθ=tanθ
01:43View Solutionsinθ−2sin3θ2cos3θ−cosθ=tanθ
01:51View SolutionIf √3tanθ=1andθ is acute, find the value of sin3θ+cos2θ
01:57View SolutionIf tanθ=43,then the value of 3sinθ+2cosθ3sinθ−2cosθ is
04:38View SolutionIf 2−cos2θ=3sinθcosθ,sinθ≠cosθ then tanθ is
View SolutionSolve the following equations:
(i) sin5x−sinx=cos3x (ii) 2cos2θ+3sinθ−3=θ
(iii) cosθ+cos3θ=2cos2θ (iv) sinθ+sin3θ+sin5θ=0
(v) sin2θ−cos2θ−sinθ+cosθ=0 (vi) sinθ+cosθ=√3
(vii) sinθ+√3cosθ=1 (viii) cotθ+ cosec θ=√3
(ix)tanθ+tan(θ+π3)+tan(θ+2π3)=√3
(x) cos2θ=√5+14 (xi) 2cos2x−7cosx+3=002:20View Solutionयदि √3tanθ=3sinθ हो, तो sin2θ−cos2θ का मान ज्ञात कीजिए |
02:08View SolutionIf √3tanθ=3sinθ, find the value of sinθ2θ−cos2θ, where θ≠0.
01:31View Solutionयदि 3cosθ−4sinθ=2cosθ+sinθ, तो tanθ का मान है
02:00View SolutionProve that
sinθ−2sin3θ2cos3θ−cosθ=tanθ03:32View Solution

