Find the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}
Video Solution
Text Solution
Let us first sketch the region whose area is to be found out. This region is the intersection of the following regions.
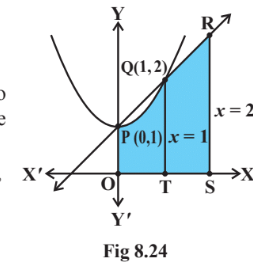
area of the region OTQPO + area of the region TSRQT
so required area is =∫10(x2+1)dx+∫21(x+1)dx
(x33+x)10+(x22+x)21
(13+1)+(4−32)
43+52=236sq unit
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
- BOOK - NCERTCHAPTER - APPLICATION OF INTEGRALSEXERCISE - MISCELLANEOUS EXERCISE19videos
APPLICATION OF INTEGRALS
- BOOK - NCERTCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.118videos
APPLICATION OF DERIVATIVES
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION3videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the area of the region.
{(x,y):y28,6x,x2+y27(6}View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View SolutionFind the area of the region {(x,y):x2≤y≤x}
View SolutionFind the area of the region {(x,y):x2≤y≤x}
View SolutionFind the area of the region {(x,y) :x2+y2≤4, x+y ≥2}
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}
View SolutionFind the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
View SolutionFind the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
View SolutionFind the area of the region {(x,y):y2≤4x,4x2+4y2≤9}
View SolutionUsing integration, find the area of the region
{(x,y):x2+y2≤1,x+y≥1,x≥0,y≥0}View Solution

