कोई भौतिक राशि P, चार प्रेक्षण - योग्य राशियों a,b,c तथा d से इस प्रकार सम्बंधित है :
P=a3b2/(√cd)
a,b,c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%,3%,4% तथा 2% है राशि P में प्रतिशत त्रुटि कितनी है ? यदि उपर्युक्त संबंध का उपयोग करके P का परिकलित मान 3⋅763 आता है, तो आप परिणाम का किस मान ताल निकटन करेंगे ?
P=a3b2√cd=a3b2e−1/2d−1
P के मान में भिन्नात्मक त्रुटि
ΔPP=3Δaa+2Δbb−12Δcc−Δdd
तथा P के मान में अधिकतम भिन्नात्मक त्रुटि
(ΔPP)अधिकतम=3Δaa+2Δbb+12Δcc+Δdd
अब P के मान में अधिकतम प्रतिशत त्रुटि
(ΔPP)अधिकतम×100=3(Δaa×100)+2(Δbb×100)+12(Δcc×100)+(Δdd×100)
3(a में प्रतिशत त्रुटि)+2(b में प्रतिशत त्रुटि)+12(c में प्रतिशत त्रुटि)+(d में प्रतिशत त्रुटि)
=3(1%)+2(3%)+12(4%)+1(2%)
=13%.
P का परिकलित मान 3⋅763 है तथा P के मान में प्रतिशत त्रुटि 13% है इस प्रकार, P के मान में त्रुटि
ΔP=3⋅763×13100=0⋅48919=0⋅5
चूँकि P के मान त्रुटि दशमलव के दायीं ओर एक अंक तक है अतः P का मान भी दशमलव के एक अंक तक P=3⋅8 होगा।
Topper's Solved these Questions
- मापन एवं मात्रक BOOK - SHIVLAAL PUBLICATIONCHAPTER - मापन एवं मात्रक EXERCISE - अतिरिक्त महत्वपूर्ण स्मरणीय तथ्य
1 Videos
- मापन एवं मात्रक BOOK - SHIVLAAL PUBLICATIONCHAPTER - मापन एवं मात्रक EXERCISE - बोधात्मक प्रश्न
7 Videos
- मापन एवं मात्रक BOOK - SHIVLAAL PUBLICATIONCHAPTER - मापन एवं मात्रक EXERCISE - संख्यात्मक प्रश्न (विमीय विश्लेषण)
7 Videos
- भौतिक जगत एवं मात्रक और मापनBOOK - SHIVLAAL PUBLICATIONCHAPTER - भौतिक जगत एवं मात्रक और मापनEXERCISE - आंकिक प्रश्न
5 Videos
- वृत्तीय गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - वृत्तीय गति EXERCISE - वस्तुनिष्ठ प्रश्न
33 Videos
Similar Questions
गज लम्बाई का मात्रक है 1 गज =0⋅9144 मीटर ।
View Solutionवेग (v), समय (T) तथा बल (F) को मूल राशि मानने पर द्रव्यमान विमाएँ लिखिए |
View Solutionवायु में ध्वनि का वेग 332 मीटर/सेकण्ड है। इसका मान किलोमीटर/घण्टा मात्रक में ज्ञात कीजिए।
View Solutionनिम्न के संख्यात्मक मान 10 की घात में लिखिए-
(i) मिली (m)
(ii) माइक्रो
(iii) गीगा (G)
(iv) पेटा (P).
View Solutionएकसमान क्षैतिज वृत्तीय गति में नियत रहता है :
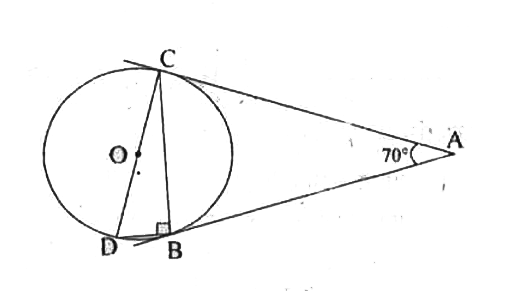
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View SolutionColumn- I Column - II (A) l का मान है (P) -6 (B) m का मान है (Q) 6 (C) n का मान है (R) 13(D) (l + m + n) का मान है (T) 42
View SolutionIf A=0.142857142857.... and B=0.16666.... then what is the value of (A+B) /AB? यदि A=0.142857142857.... तथा B=0.16666.... है ,तो (A+B)/AB का मान क्या है?
View SolutionThe average of two numbers A and B is 20, that of B and C is 19 and of C and A it is 21. What is the value of A? दो संख्याओं A तथा B का औसत 20, B तथा C का औसत 19 और C तथा A का औसत 21 है। A का मान क्या है?
View SolutionIf 7129p465 is divisible by 9, then the value of p is:
यदि 7129p465 , 9 से विभाज्य है, तो p का मान है:
View SolutionThe average of a, b and c is 9. The average of b and c is 10. What is the value of a?
a, b तथा c का औसत 9 है | b तथा c का औसत 10 है | a का मान कितना है ?
View SolutionA sum of Rs. x is divided among A , B and C such that the ratio of shares of A and B is 7: 12 and that of B and C 1s 8: 5. If the difference in the shares of A and C is Rs. 214 , then the value of x is:
x रुपये की राशि A , B और C में इस प्रकार विभाजित की जाती है कि A और B के हिस्से का अनुपात 7 : 12 है और B तथा C के हिस्से का अनुपात 8 : 5 है | यदि A और C के हिस्सों में 214 रुपये का अंतर है, तो x का मान ज्ञात करें |
View SolutionA sum of Rs. x is divided among A, B and C such that the ratio of the shares of A and B is 6:7 and that of B and C is 3:2. If the difference between the shares of A and C is Rs. 540, then the value of x is :
x रुपये की राशि A, B और C में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 6 : 7 है तथा B और C के हिस्सों का अनुपात 3 :2 है | यदि A और C के हिस्सों में 540 रुपये का अंतर है, तो x का मान क्या होगा ?
View SolutionA sum is divided among A, B, C and D such that the ratio of shares of A and B is 2:3, that of B and C is 1:2 and that of C and D is 3:4. If the difference between the shares of A and D is Rs. 648, then the sum of their shares is :
एक राशि A, B, C और D में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 2 : 3 है तथा B और C के हिस्सों का अनुपात 1: 2 है और C एवं D के हिस्सों का अनुपात 3 : 4 है| यदि A और D के हिस्सों में 648 रुपये का अंतर है, तो उनके हिस्सों का योग ज्ञात करें |
View SolutionIf a : b = 2 : 3 and c : b = 5 : 6 , then a : b : c is equal to:
यदि a : b = 2 : 3 तथा c : b = 5 : 6 है, तो a : b : c का मान ज्ञात करें |
View Solution
