Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If A is obtuse angle I ABC, then tanB tanC<1 because Statement II: In ABC, tanA=tanB+tanCtanBtanC−1 a.A b. B c. C d. D
Step by step video & image solution for Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If A is obtuse angle I A B C , then tanB\ t a n C<1 because Statement II: In A B C ,\ t a n A=(t a n B+t a n C)/(t a n B t a n C-1)\ a.A b. \ B c.\ C d. D by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: tan5θ−tan3θ−tan2θ=tan5θtan3θtan2θ Statement II: x=y+z⇒tanx−tany−tanz=tanxtanytanz. a.A b. B c. C d. D
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true 2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If a, b,c∈R anda≠b≠c and x, y, z are non zero. Then the system of equations ax+by+cz=0bx+cy+az=0cx+ay+bz=0 has infinite solutions. because Statement II: If the homogeneous system of equations has non trivial solution, then it has infinitely many solutions. a.A b. B c. C d. D
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If (log)((log)5x)5=2, thn x=5√5 Statement II: (log)xa=b, if a>0, then x=a1/b a.A b. B c. C d. D
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: sec2θ=4xy(x+y)2 is positive for all real values of x and y oly when x=y because Statement II: t2≥0∀t∈R a.A b. B c. C d. D
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If a=y2, b=z2,c=x2, then8(log)ax3.logby3.logcz3=27 Statement II: (log)ba.logcb=(log)ca, also (log)ba=1logab a.A b. B c. C d. D
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: the equation (log)12+|x|(5+x2)=(log)(15+√x) has real solutions. Because Statement II: (log)1/ba=(log)ba (where a, b>0 and b≠1) and if number and base both are greater than unity then the number is positive. a.A b. B c. C d. D
View SolutionStatement I is True: Statement II is True; Statement II is a correct explanation for statement I Statement I is true, Statement II is true; Statement II not a correct explanation for statement I. Statement I is true, statement II is false Statement I is false, statement II is true Statement I: coses−1(cosec95)=π−95. because Statement II: cosec−1(cosecx)=π−x: ∀x∈[π2,3π2]−{π} a.A b. B c. C d. D
View SolutionStatement I is True: Statement II is True; Statement II is a correct explanation for statement I Statement I is true, Statement II is true; Statement II not a correct explanation for statement I. Statement I is true, statement II is false Statement I is false, statement II is true Let f:R→R [0, π/2] defined by f(x)=tan−1(x2+x+a) , then Statement I: The set of values of a for which f(x) is onto is [14,∞) because Statement II: Minimum value of x2+x+a is a−14. a.A b. B c. C d. D
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: Yield of R-Br follows the order 1∘>2∘>3∘ in Hundsdicker reaction
Statement -2: Hundsdicker reaction follows free redical mechanism.
View SolutionEach question has 5 choices (a) ,(b) ,(c ) (d) and (e ) out of which ONLY ONE is correct.
(a) Statement -1 is True, Statement -2 is True , Statement -2 is a correct explanation for Statement -1.
(b) Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1.
(C ) Statement -1 is True, Statement -2 is False.
(d) Statement -1 is False, Statement -2 is True.
(e) Statement -1 and Statement -2 both are False.
Statement -1: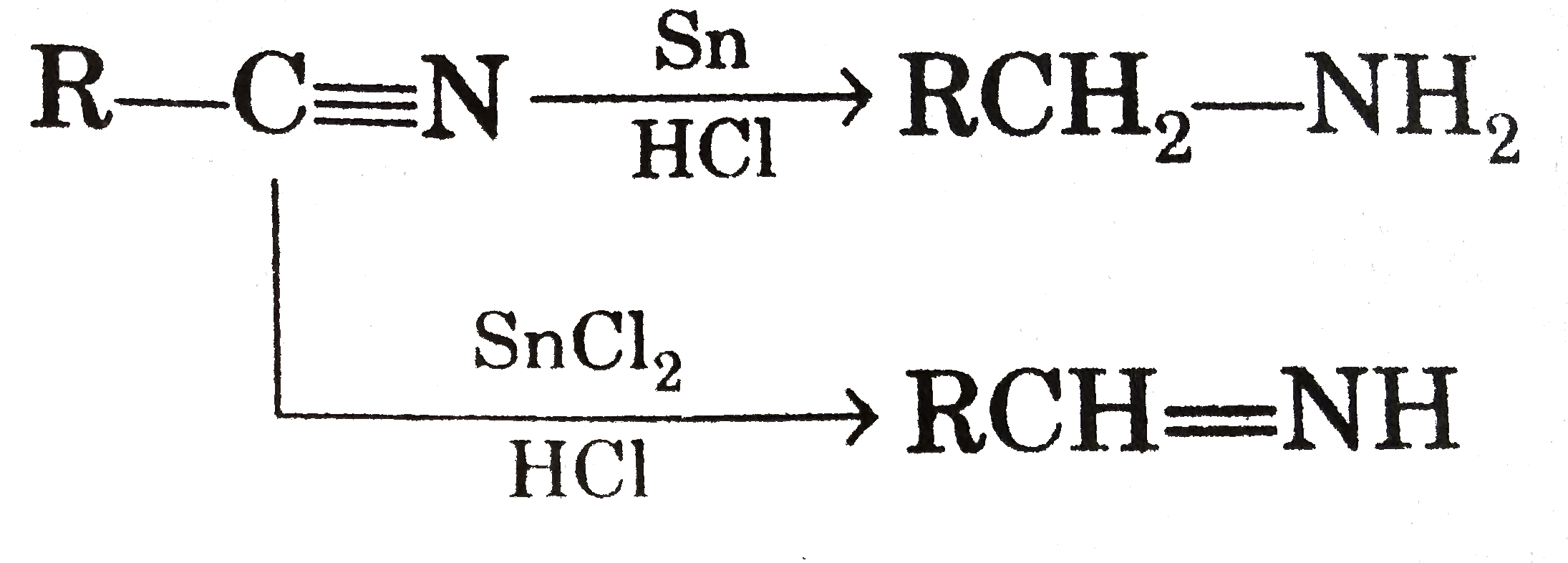
Statement-2: Sn can give maximum of 4 electron during reduction, whereas SnCl2 can give only 2.
View Solution
