A and B are moving in two circular orbits with angular velocity
respectively. Their position are shown at t = 0. Find the time at which they will meet for 1st time
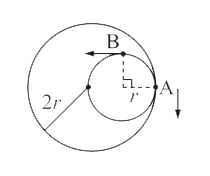
They will never meet
The correct Answer is:D
They can meet only at the initial position of A.
time after which A reach this position
time after which B reach this position
They will never be able to meet as for no value of and these two terms will be same.
Similar Questions
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
 View Solution
View SolutionTwo particle 'A' and 'B' are moving on the same circle with angular ω1 and ω2 respectively w.r.t. the centre of circle. Find the angular velocity of 'A' w.r.t. 'B' when,
(i) their sense of rotations is same,
(ii) and their sense of rotation is opposite.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a circular path of radius R with an angualr velocity ω=a−bt, where a and b are positive constants and t is time. The magnitude of the acceleration of the particle after time 2ab is
AaRBa2RCR(a2+b)DR√a4+b2 - Question 2 - Select One
A conical pendulum is moving in a circle with angular velocity ω as shown. If tension in the string is T, which of following equations are correct ?
 AT=mω2lBTsinθ=mω2lCT=mgcosθDT=mω2lsinθ
AT=mω2lBTsinθ=mω2lCT=mgcosθDT=mω2lsinθ - Question 3 - Select One
A particle is moving in a circular orbit of radius r1 with an angular velocity ω1 It jumps to another circular orbit of radius r2 and attains an angular velocity ω2 . If r2=0.5r1 , and if no external torque is applied to the system, then the new angular velocity ω2 is given by
Aω2=ω1Bω2=2ω1Cω2=3ω1Dω2=4ω1
Two particles A and B are moving in a horizontal plane anticlockwise on two different concentric circles with different constant angular velocities 2ω and ω,respectively. Find the relative velocity (in' ms ) of B w.r.t. A after time t=πω.(Takeomega=3 rad / s, r=2)
'(##CEN_KSR_PHY_JEE_C07_025_Q14##)'View SolutionTwo particles A and B are moving in a horizontal plane anitclockwise on two different concentric circles with different constant angular velocities 2ω and ω respectively. Find the relative velocity (in m/s) of B w.r.t. A after tome t=π/ω. They both start at the position as shown in figure (Takeω=3rad/sec,r=2m)
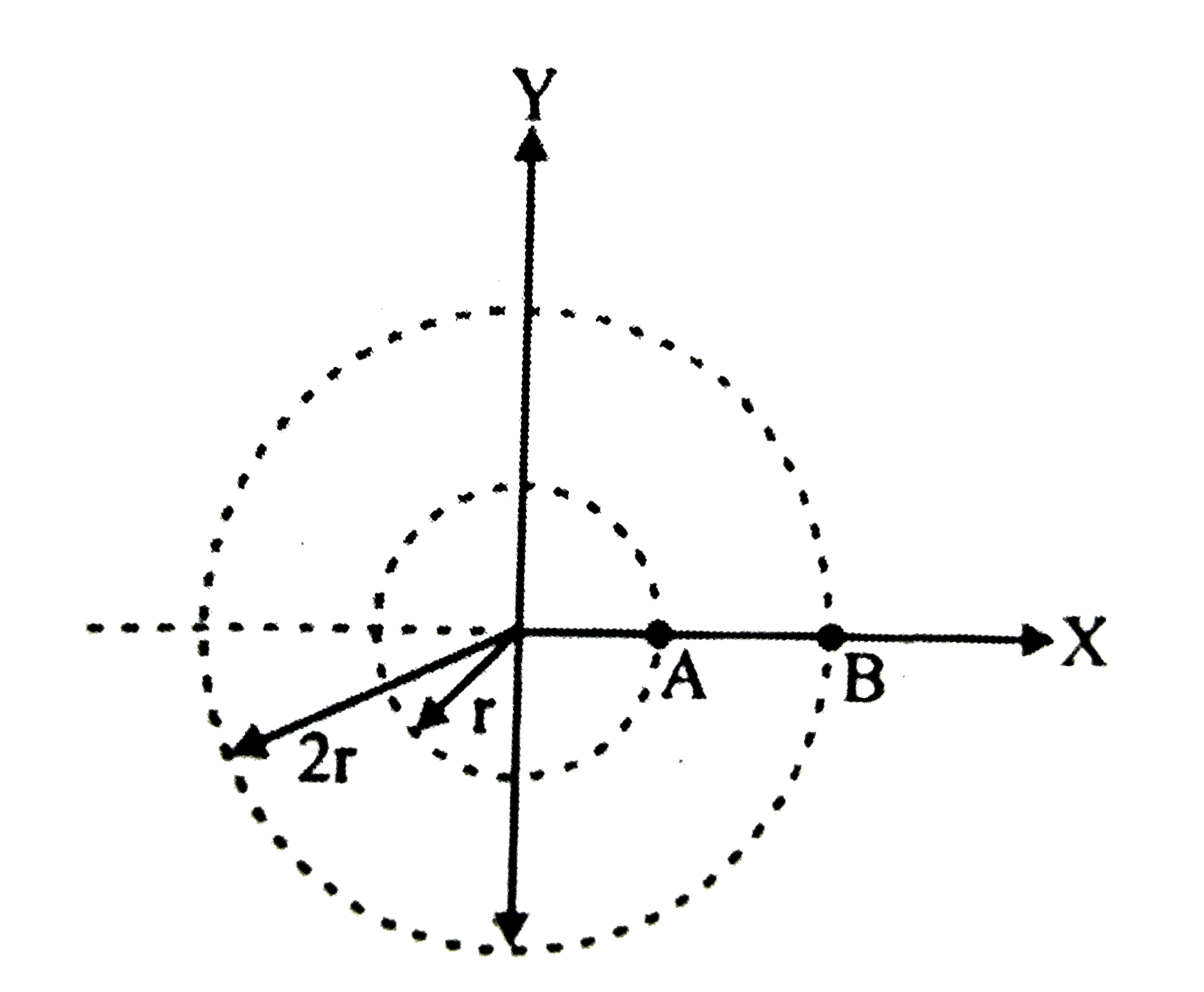 View Solution
View Solutiontwo train A and B are moving on parallel tracks with velocities of 60kmh−1and90kmh^(-1) respectively but in oppiste directions. Find (i) the relative velocity of train A.w.r.t train B and (ii) the relative velocity of ground w.r.t tain A.
View SolutionA particle executes SHM with amplitude A and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.
View SolutionIf a particle goes round the circle once in a time period T, then the angular velocity ω will be
View Solution

