A boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that the boy can throw the same stone up to will be:
m
m
The correct Answer is:D
To solve the problem of finding the maximum horizontal distance a boy can throw a stone given that he can throw it to a maximum height of 10 m, we can follow these steps:
1. Understand the Maximum Height:
The maximum height (h_max) that the boy can throw the stone is given as 10 m. This height is achieved when the stone is thrown vertically upwards.
2. Use the Kinematic Equation:
We can use the kinematic equation for vertical motion to relate the initial velocity (u), final velocity (v), acceleration (a), and displacement (s):
v2=u2+2as
At the maximum height, the final velocity (v) is 0 m/s, the acceleration (a) is -g (where g = 10 m/s²), and the displacement (s) is 10 m.
3. Set Up the Equation:
Plugging in the values into the equation:
0=u2−2g⋅hmax
Rearranging gives:
u2=2ghmax
4. Calculate the Initial Velocity:
Substituting g = 10 m/s² and h_max = 10 m:
u2=2⋅10⋅10=200
Therefore, the initial velocity (u) is:
u=√200=10√2 m/s
5. Determine the Maximum Range:
The range (R) of a projectile is given by the formula:
R=u2sin(2θ)g
For maximum range, the angle of projection (θ) should be 45 degrees, where sin(90°) = 1. Thus, the formula simplifies to:
R=u2g
6. Substitute the Values:
Now substituting u² = 200 and g = 10:
R=20010=20 m
Final Answer:
The maximum horizontal distance that the boy can throw the stone is 20 meters.
The maximum height (h_max) that the boy can throw the stone is given as 10 m. This height is achieved when the stone is thrown vertically upwards.
We can use the kinematic equation for vertical motion to relate the initial velocity (u), final velocity (v), acceleration (a), and displacement (s):
v2=u2+2as
At the maximum height, the final velocity (v) is 0 m/s, the acceleration (a) is -g (where g = 10 m/s²), and the displacement (s) is 10 m.
Plugging in the values into the equation:
0=u2−2g⋅hmax
Rearranging gives:
u2=2ghmax
Substituting g = 10 m/s² and h_max = 10 m:
u2=2⋅10⋅10=200
Therefore, the initial velocity (u) is:
u=√200=10√2 m/s
The range (R) of a projectile is given by the formula:
R=u2sin(2θ)g
For maximum range, the angle of projection (θ) should be 45 degrees, where sin(90°) = 1. Thus, the formula simplifies to:
R=u2g
Now substituting u² = 200 and g = 10:
R=20010=20 m
The maximum horizontal distance that the boy can throw the stone is 20 meters.
Similar Questions
A man can throw a stone with initial speed of 10m/s. Find the maximum horizontal distance to which he can throw the stone in a room of height h m for:
(i) h=2m and (ii) h=4m.View SolutionThe greatest height to which a boy can throw a stone is (h). What will be the greatest distance on horizontal surface upto which the boy can throw the stone with the same speed ? Neglect the air friction.
View Solution
Knowledge Check
- Question 1 - Select One
A person can throw a stone to a maximum height of h meter. The maximum distance to which he can throw the stone is:
AhBh/2C2hD3h - Question 2 - Select One
A man can throw a stone to a maximum distance of 80 m. The maximum height to which will rise,
A30mB20mC10mD40m - Question 3 - Select One
A person can throw a stone to a maximum distance of h meter. The greatest height to which he can throw the stone is:
AhBh/2C2hD3h
A person can throw a ball vertically upto maximum height of 20 mt. How far can he throw the ball.
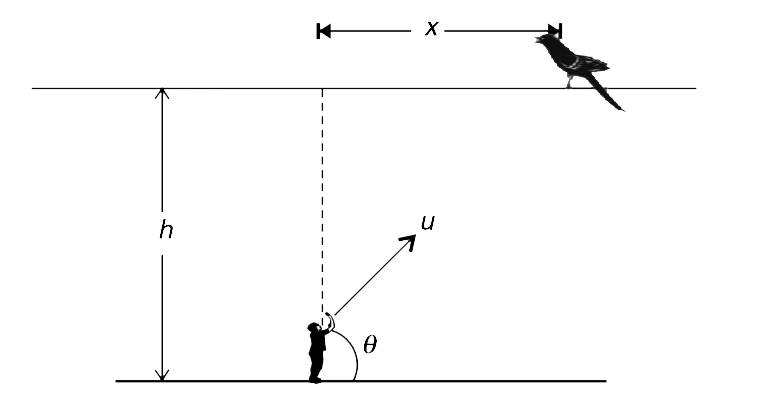
View SolutionA horizontal electric wire is stretched at a height h=10m above the ground. A boy standing on the ground can throw a stone at a speed u=20ms–1. Find the maximum horizontal distance x at which a bird sitting on the wire can be hit by the stone.
 View Solution
View SolutionA man can throw a stone 80 meters. The maximum height to which it will rise in meters is
View SolutionA student is able to throw a ball vertically to maximum height of 40m. The maximum distance to which the student can throw the ball in the horizonal direction:-
View SolutionIf a person can throw a stone to maximum height of h metre vertically, then the maximum distance through which it can be thrown horizontally by the same person is
View Solution

