A block of mass m placed on the inclined surface of wedge of mass M. Block is clamped between two smooth vertical support such that it can move along vertical If all contact surface are smooth then acceleration of wedge is:

The correct Answer is:B
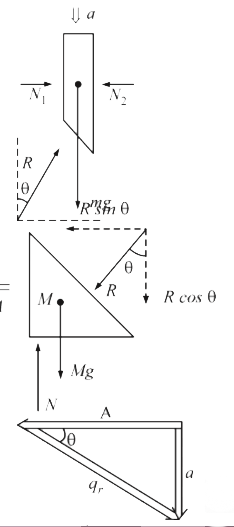
…(i)
…..(ii)
….(iii)
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
All surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 2 - Select One
All surfaces are smooth. The acceleration of mass m relative to the wedge is
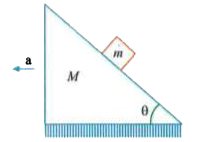 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 3 - Select One
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
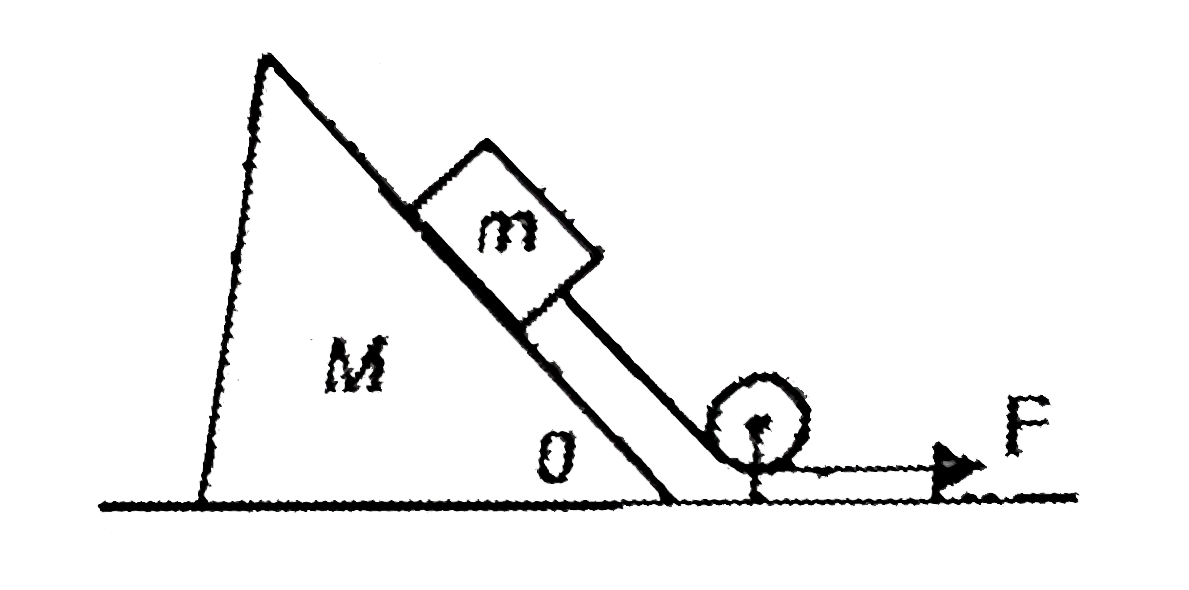 View Solution
View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.
 View Solution
View SolutionA block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionIn the arrangement shown in figure wedge of mass M moves towards left with an acceleration a. All surfaces are smooth. The acceleration of mass m relative to wedge is
 View Solution
View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
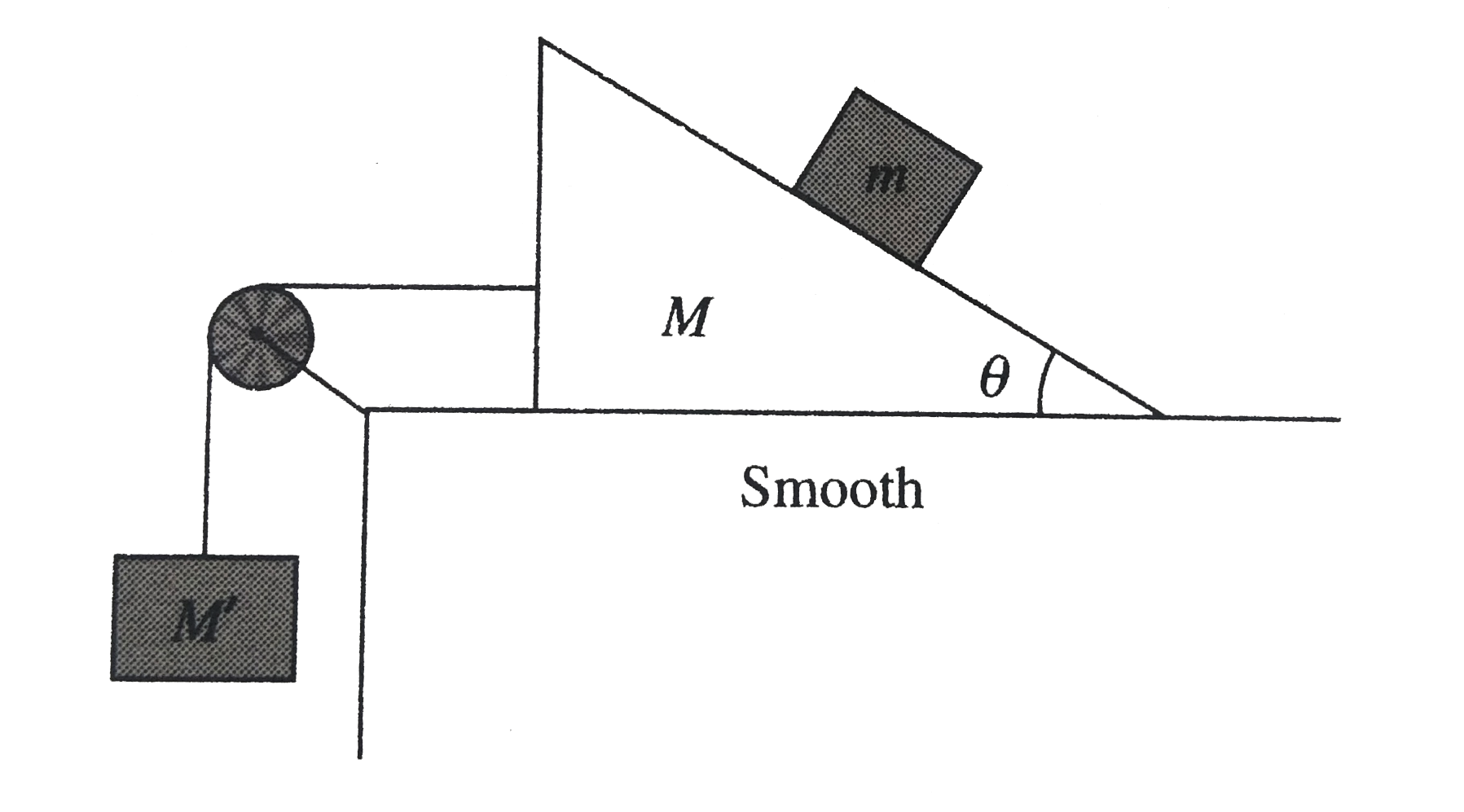 View Solution
View Solution

