A spherical shell has inner radius R1, outer radius R2, and mass M, distributed uniformly throughout the shell. The magnitude of the gravitational force exerted on the shell by a point mass particle of mass m, located at a distance d from the center, inside the inner radius, is:
0
GMm/R21
GMm/d2
GMm/(R22−d2)
The correct Answer is:A
To solve the problem, we need to determine the gravitational force exerted on a point mass m located inside a spherical shell with inner radius R1, outer radius R2, and mass M uniformly distributed throughout the shell.
1. Understanding the Setup:
- We have a spherical shell with inner radius R1 and outer radius R2.
- A point mass m is located at a distance d from the center of the shell, where d<R1 (inside the shell).
2. Applying Gauss's Law for Gravitation:
- According to Gauss's Law for gravitation, the gravitational field Eg at a distance r from the center of a spherical shell is determined by the mass enclosed within that radius.
- For a Gaussian surface inside the shell (where r<R1), the mass enclosed is zero because all the mass M is distributed in the shell itself.
3. Calculating the Gravitational Field:
- Since there is no mass enclosed within the Gaussian surface, we have:
Eg=0
- This means that the gravitational field inside the shell is zero.
4. Calculating the Gravitational Force:
- The gravitational force F on the mass m can be calculated using the formula:
F=m⋅Eg
- Substituting Eg=0:
F=m⋅0=0
5. Conclusion:
- The magnitude of the gravitational force exerted on the point mass m located inside the inner radius of the shell is:
F=0
Final Answer:
The gravitational force exerted on the mass m by the spherical shell is 0.
---
- We have a spherical shell with inner radius R1 and outer radius R2.
- A point mass m is located at a distance d from the center of the shell, where d<R1 (inside the shell).
- According to Gauss's Law for gravitation, the gravitational field Eg at a distance r from the center of a spherical shell is determined by the mass enclosed within that radius.
- For a Gaussian surface inside the shell (where r<R1), the mass enclosed is zero because all the mass M is distributed in the shell itself.
- Since there is no mass enclosed within the Gaussian surface, we have:
Eg=0
- This means that the gravitational field inside the shell is zero.
- The gravitational force F on the mass m can be calculated using the formula:
F=m⋅Eg
- Substituting Eg=0:
F=m⋅0=0
- The magnitude of the gravitational force exerted on the point mass m located inside the inner radius of the shell is:
F=0
The gravitational force exerted on the mass m by the spherical shell is 0.
Similar Questions
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroDGMMR2 - Question 2 - Select One
A point mass 'm' is placed inside a spherical shell of radius 'R' and mass 'M' at a distance from the centre of the shell. The gravitational force exerted by the shell on the point mass is -
AGMmR2B2GMmR2CzeroD4GMmR2 - Question 3 - Select One
A particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
A−3GMaB−2GMaC−GMaD−4GMa
Find the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA nonconducting sphere with radius a is concentric with and surrounded by a conducting spherical shell with inner radius b and outer radius c. The inner sphere has a negative charge uniformly distributed throughout its volume, while the spherical shell has no net charge. The potential V (r) as a function of distance from the center is given by
 View Solution
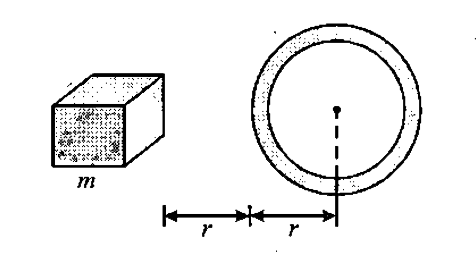
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
 View Solution
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
View Solution

